IND01.Introduzione ai sistemi di controllo

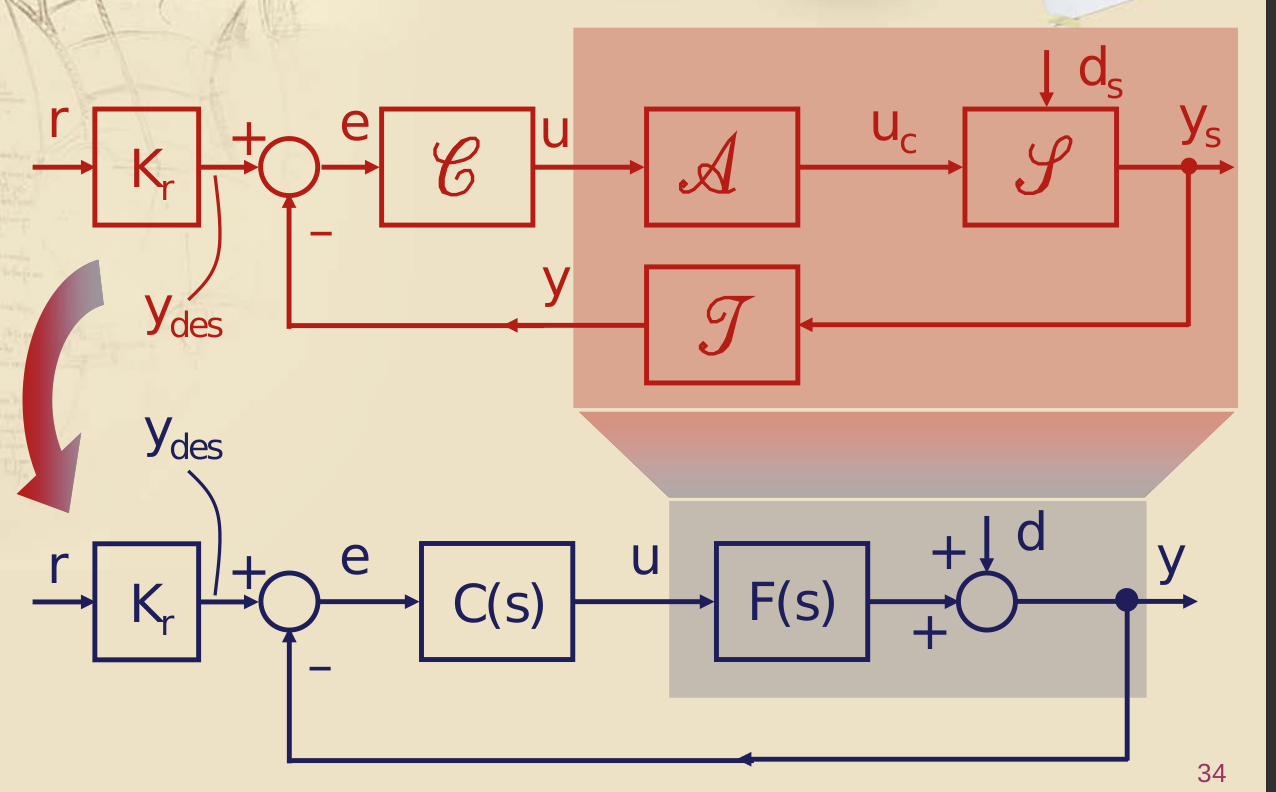
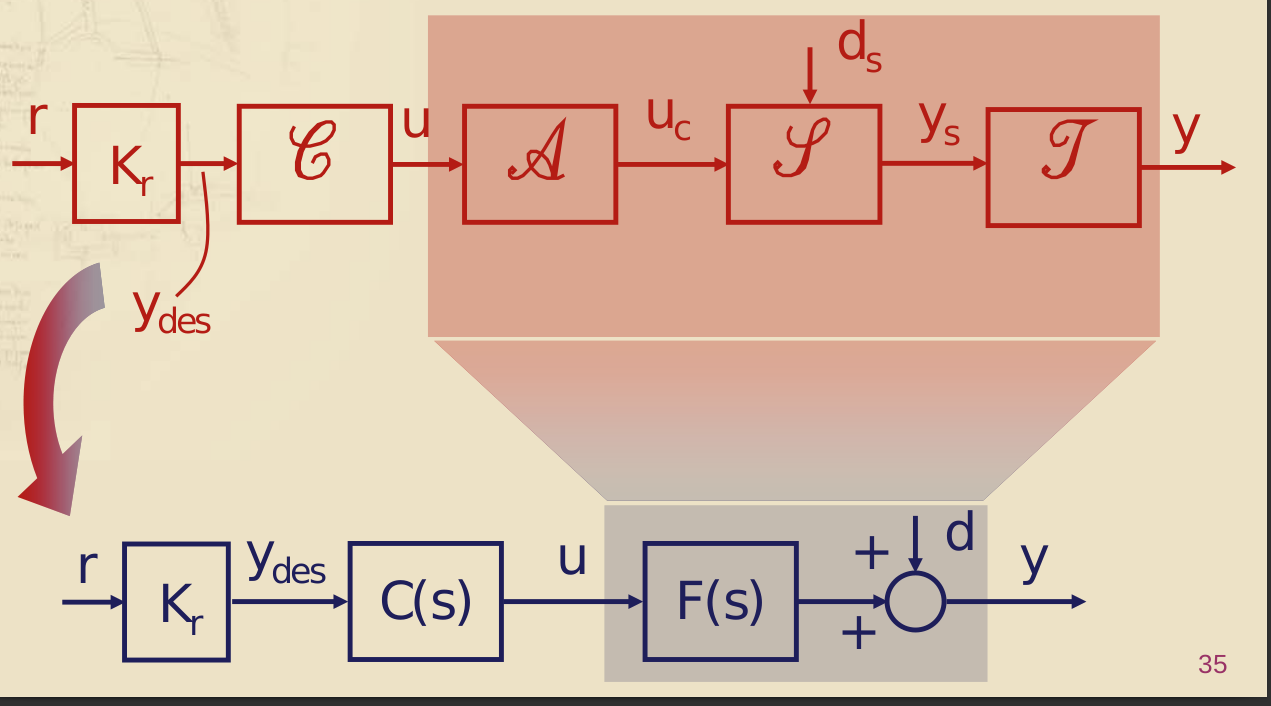
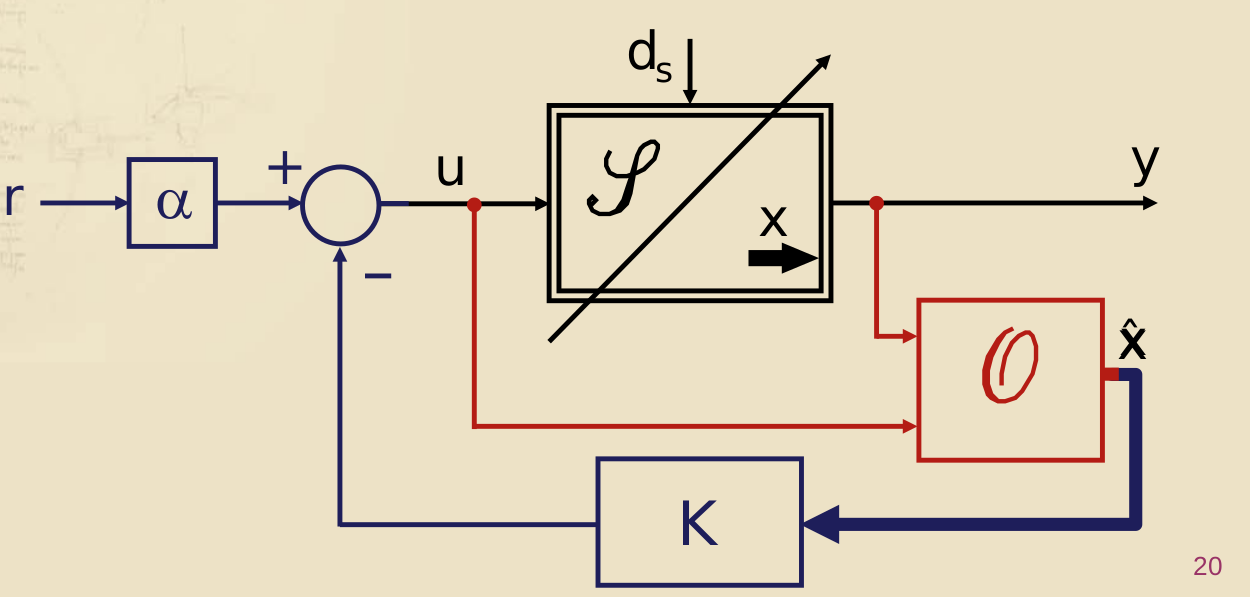
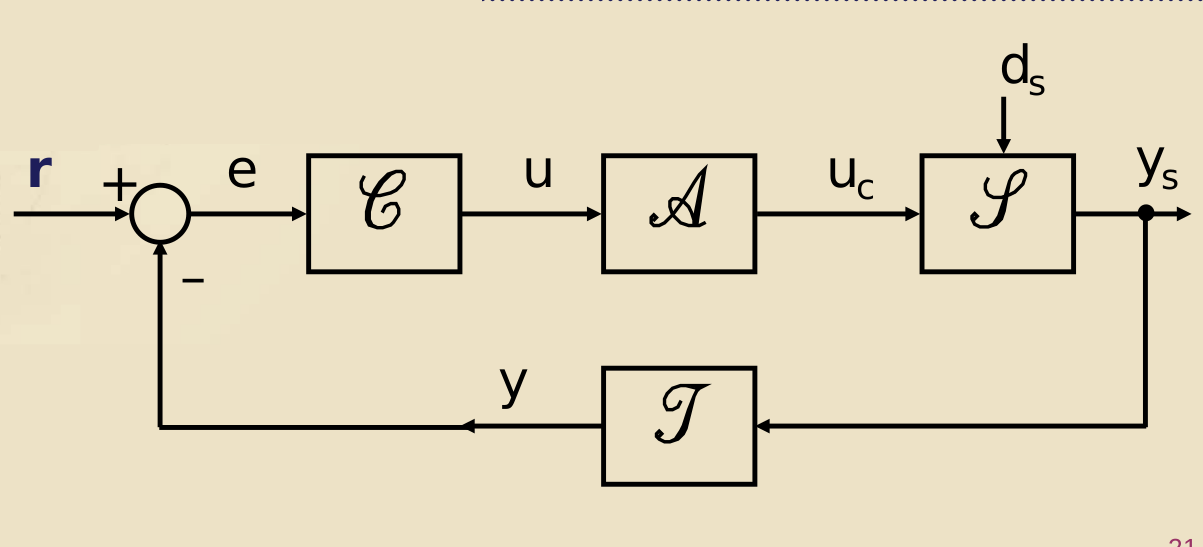
Elementi comuni ai sistemi di controllo

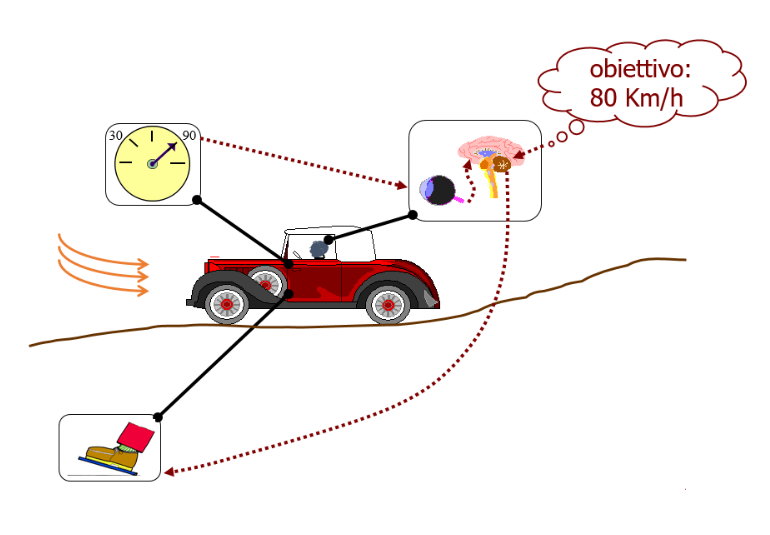
• Sistema: ha come ingressi disturbi e una variabile di comando $u_C$, ha un’uscita di interesse soggetta a controllo $y_S$ e degli stati interni non sempre accessibili e misurabili $x$
  • nell’esempio, massa dell’auto; $y_S$ è la velocità dell’auto; $u_C$ è la forza sprigionata dal motore
• Azionamento / attuatore: ha come ingresso una variabile di controllo ad energia trascurabile $u$ (spesso una tensione), come uscita la variabile di comando del sistema $u_C$ (spesso un’altra tensione, ma che entra nel sistema vero e proprio quindi è dimensionata correttamente per ottenere gli effetti voluti). Questi sono già disponibili sul mercato, quindi non è necessario progettarli da zero.
  • nell’esempio, motore dell’autoveicolo; $u_C$ è la forza sprigionata dal motore; $u$ è la posizione dei pedali
• Trasduttore: ha come ingresso la variabile di uscita del sistema $y_S$ e come uscita la misura $y$ della stessa $y_S$ (ad energia trascurabile) (quindi tecnicamente una tensione il cui valore mi identifica il valore attuale della reale uscita del sistema, magari quantizzato). Idealmente è lineare, statico, a parametri concentrati, senza disturbi. Già disponibile sul mercato.
  • nell’esempio, il tachimetro; $y_S$ è la reale velocità istantanea dell’auto, $y$ è una sua misura
• Riferimento: $r$ spesso coincide con l’uscita desiderata $y_{\text{des}}$. Se costante, ciò che il controllore esegue è detto regolazione. Se non costante, il sistema è costretto dal controllore ad inseguirlo, quindi ciò che il controllore risolve è il problema dell’inseguimento di un segnale.
  • nell’esempio, velocità obiettivo ($80$ Km/h)
• Nodo di confronto: ha come ingressi le variabili $y_{\text{des}}$ e $y$ e ha come uscita un segnale di errore $e$. Effettua una differenza (che identifica l’attuale scarto tra ciò che vorrei in uscita e ciò che effettivamente ho in uscita ora come ora). Idealmente è lineare, statico, a parametri concentrati, senza disturbi.
  • nell’esempio, $y_{\text{des}}$ è $80$ Km/h, $y$ è la velocità segnata in questo momento dal tachimetro
• Controllore: ha in ingresso il segnale di errore $e$ e in uscita il segnale di controllo $u$ dell’attuatore. Può essere analogico o digitale.
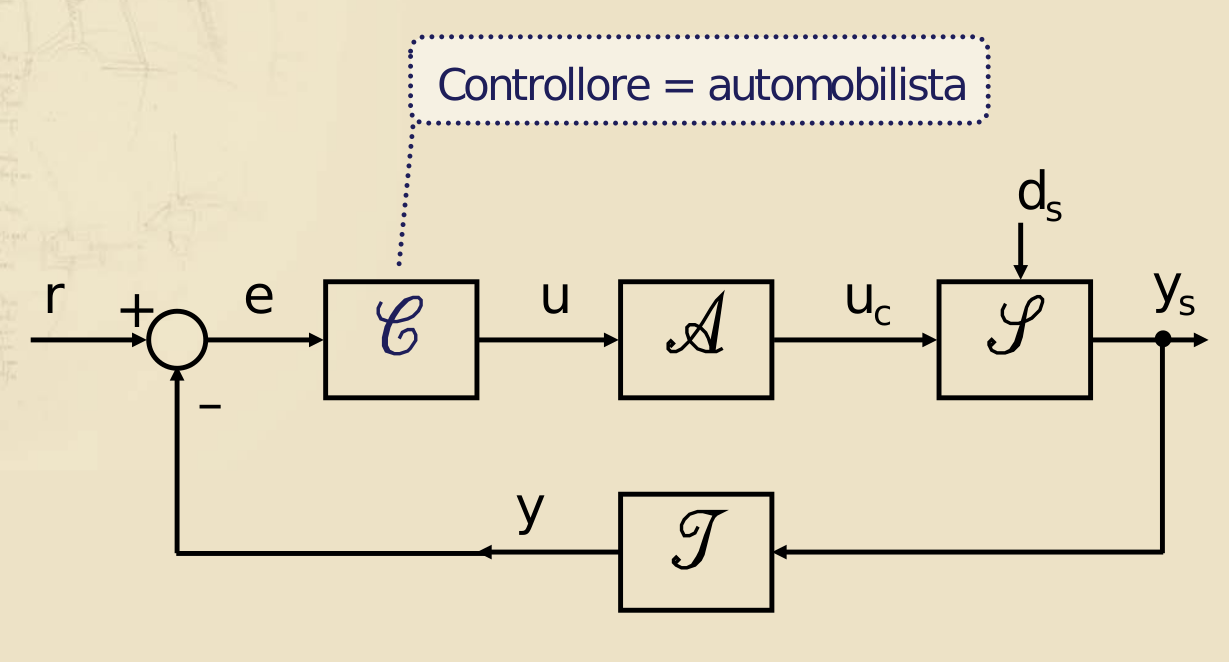
  • nell’esempio, l’automobilista è il controllore
• Sistemi di monitoraggio: diagnostica, allarmi, backup dei dati.

Esempio: l’automobile.

Info

Molto spesso (praticamente sempre) noi considereremo i componenti attuatore e trasduttore come interni al sistema stesso e perciò nascosti a noi. Per noi il controllore fornirà un $u$ che entrerà nel sistema, da cui uscirà una $y$

(^^ catena aperta)

Info

Differenza tra i sistemi della seconda parte del corso (Indri) e i sistemi della prima parte del corso (Taragna)
Nella seconda parte del corso non consideriamo mai gli stati interni del sistema; prendiamo in considerazione solo sistemi comoletamente raggiungibili e controllabili (in forma minima), su cui quindi possiamo imporre la stabilità tramite un controllore (automaticamente, sia stabilità asintotica interna che stabilità esterna). Infatti, nello schema di controllo non troviamo più la retroazione degli stati, per cui non ci serve più nemmeno lo stimatore asintotico per stimare lo stato a partire da ingresso e uscita del sistema: invece opereremo tramite retroazione dell’uscita.

(^^ parte di Taragna, retroazione dello stato)

(^^ parte di Indri, retroazione dell’uscita)

Inoltre parleremo sempre e solo di sistemi LTI TC MIMO. Definiremo il sistema sempre tramite la sua funzione di trasferimento tra ingresso e uscita e mai tramite le matrici dello stato o le equazioni di stato.

Algebra degli schemi a blocchi

Ci sarà utile saper disegnare un sistema secondo un diagramma a blocchi e saper ricavare la funzione di trasferimento di un sistema di cui abbiamo solo il disegno.

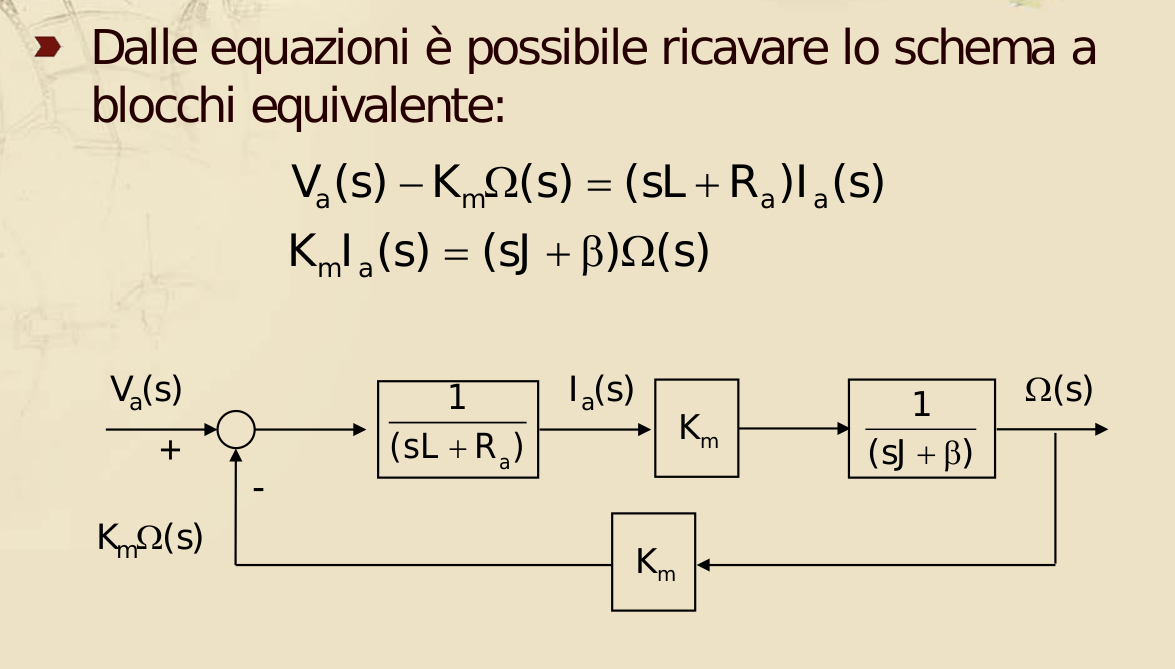
Per farlo abbiamo bisogno di conoscere alcune regole di algebra dei blocchi:

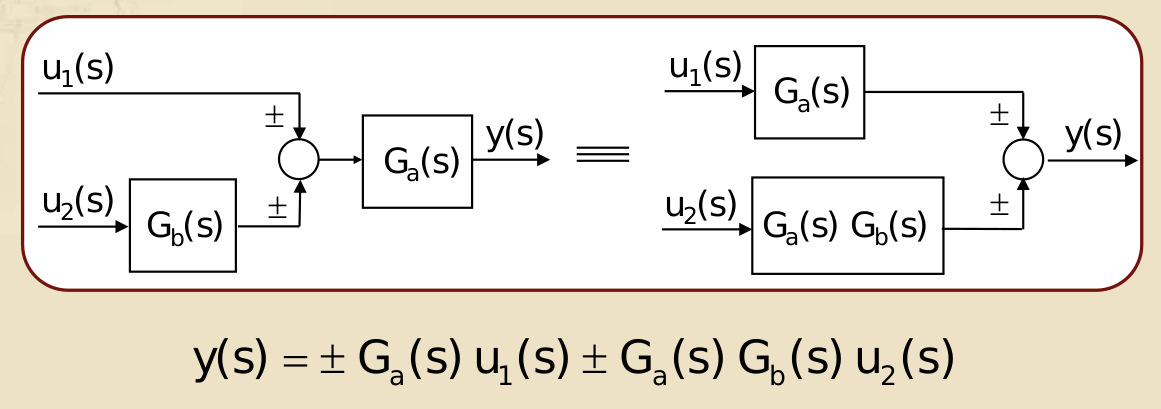
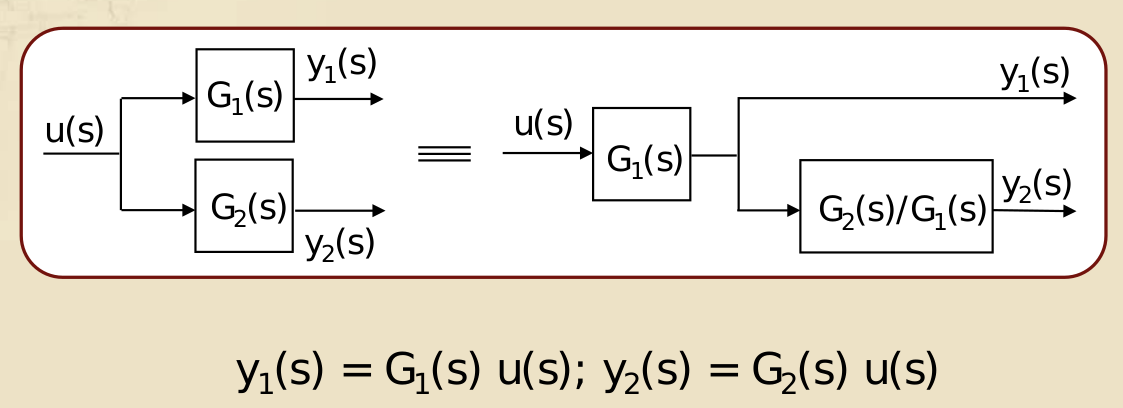
• Blocchi in parallelo sommano le loro FdT
• Blocchi in serie moltiplicano le loro FdT
• Regola di spostamento di un blocco rispetto ad un nodo di somma
  • Da monte a valle
    • 
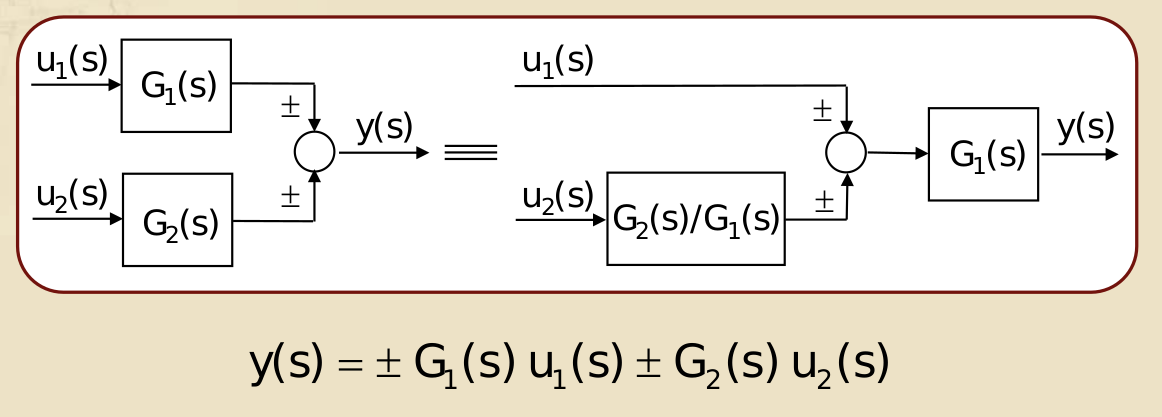
    • Da valle a monte
      • 
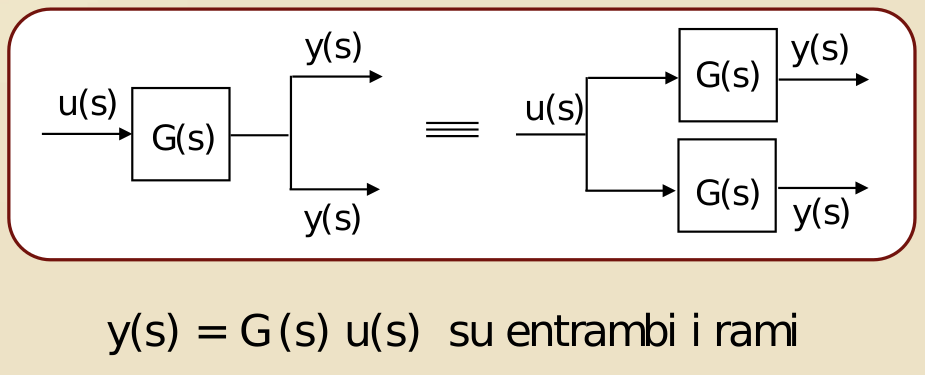
• Regola di spostamento di un blocco rispetto ad un punto di derivazione
  • Da monte a valle
    • 
  • Da valle a monte
    • 
• Regola per il calcolo della funzione di trasferimento di un anello chiuso in retroazione
  • 
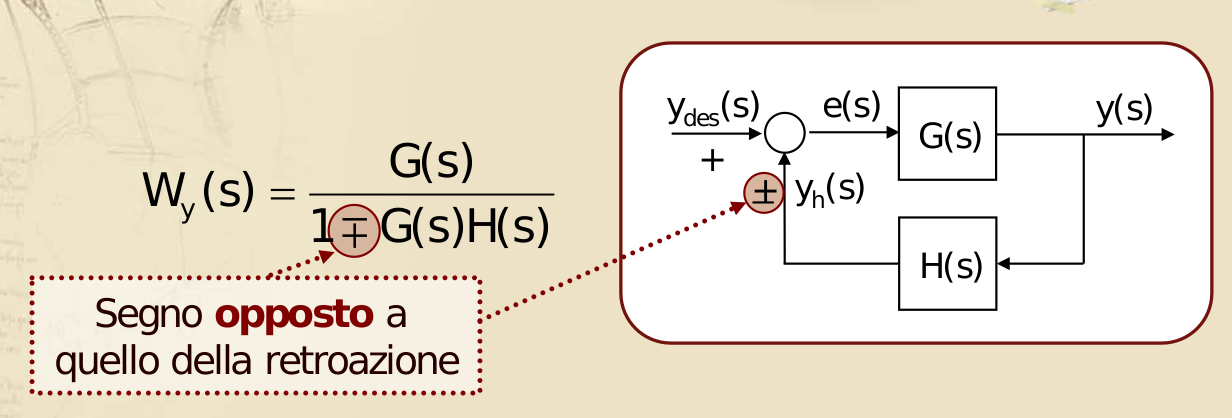
  • $G(s)$ è la FdT del ramo diretto
  • $H(s)$ è la FdT del ramo in retroazione
  • $G(s)H(s):=G_a(s)$, detta funzione d’anello o FdT della catena aperta

Cosa particolare che servirà tra un po’

Questo schema

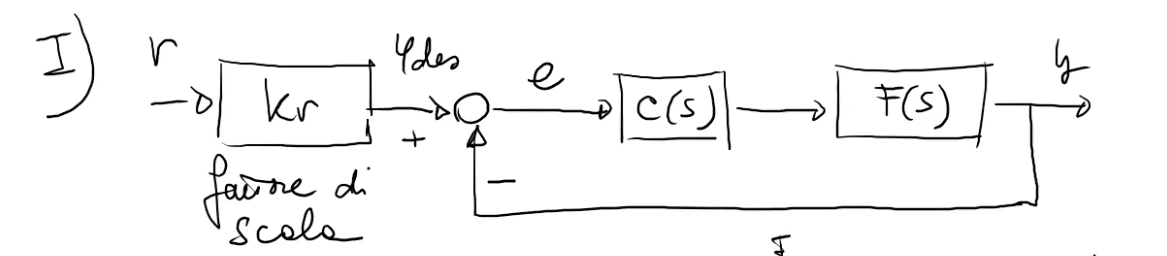
è equivalente a

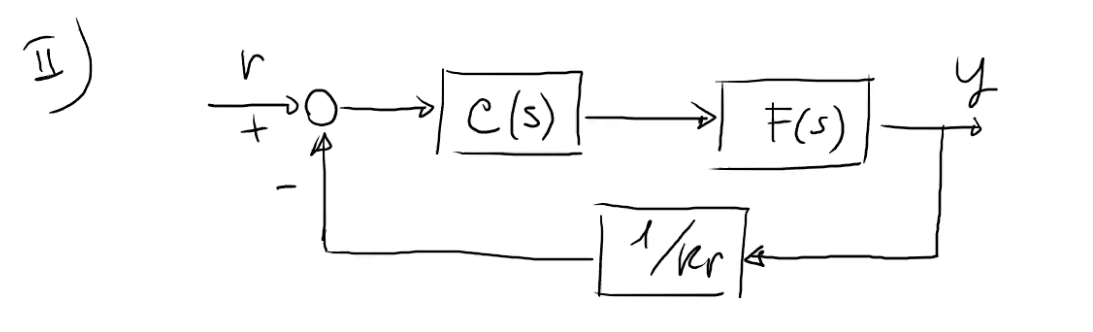
tramite la regola per lo spostamento del blocco $K_r$ rispetto al nodo di somma. Useremo molto più questo schema che quello di prima.
La funzione d’anello, però, così facendo viene ridefinita, e diventa $G_a(s)=\frac{C(s)F(s)}{K_r}$.
Il segnale $e$ ora è sostituito da $e/K_r$, detto errore ridotto.
La funzione di trasferimento della catena chiusa sarà $W(s)=\frac{y(s)}{r(s)}=\frac{C(s)F(s)}{1+G_a(s)}$ cioè $\frac{K_r{G}_a(s)}{1+G_a(s)}$.
Allora chiameremo la funzione di trasferimento di questo schema, appunto, $W$, e chiameremo quella dello schema di prima $W_y$.

Danger

Nel materiale c’è un confronto tra il primo e il secondo schema per quanto riguarda le specifiche in regime permanente. Occhio qunidi: magari prendi appunti solo sulle cose relative al secondo schema.

Specifiche di progetto

Nel realizzare il controllore per il sistema, l’unica specifica che il sistema in catena chiusa dovrà obbligatoriamente rispettare è la asintotica stabilità. Altre caratteristiche del sistema possono essere oggetto di specifica, in particolare:

• La robustezza della stabilità del sistema in catena chiusa
• Specifiche nel dominio del tempo, quindi su determinate caratteristiche della risposta del sistema, nel transitorio iniziale come in regime permanente
• La capacità di reagire in maniera ottimale ai disturbi, minimizzandone gli effetti o reiettandoli completamente

Specifiche sul regime permanente

Vedi IND03.Analisi approfondita delle specifiche di progetto > Precisione in regime permanente.

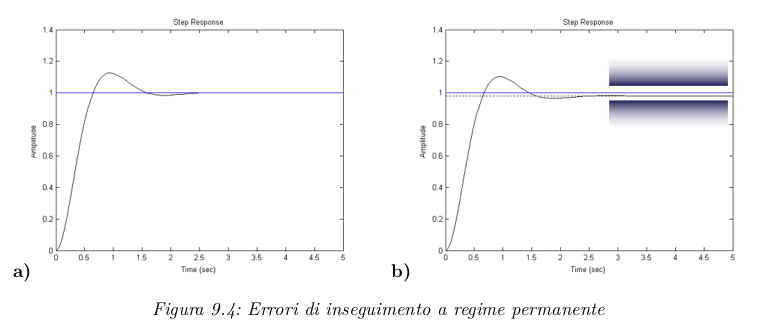
Se il sistema è stabile, allora ha un regime permanente e si può definire un valore di regime $y_{\infty }$.
Si definisce precisione di un sistema la specifica di progetto che imporne che il sistema debba dare in output un $y_{\infty }$ uguale ad un valore noto (anche nullo) scelto in precedenza, o al massimo discostarsi da esso di un $e_{\max }$ anch’esso noto (avere un errore di inseguimento $|y_{\text{des}}-y_{\infty }|\le e_{\max }$).

Specifiche sulla risposta in transitorio

Vedi IND03.Analisi approfondita delle specifiche di progetto > Risposta transitoria.

Nella maggior parte dei casi stiamo parlando di vincoli elaborati considerando ingressi particolari e “patologici”, perchè mettono realmente il controllore alla prova; principalmente, noi considereremo specifiche sulla risposta al gradino, che essendo una funzione che salta istantaneamente dal valore nullo ad un valore costante di regime è sicuramente il caso peggiore contro cui il nostro controllore debba combattere.
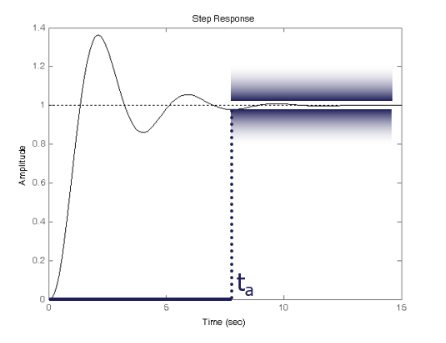
Nel caso di sistemi di ordine dal secondo in poi, la risposta del sistema nel dominio del tempo potrà avere una sovraelongazione, per cui si potrà parlare di una sovraelongazione massima \hat{s}={(y_\max-y_\infty)}/y_\infty

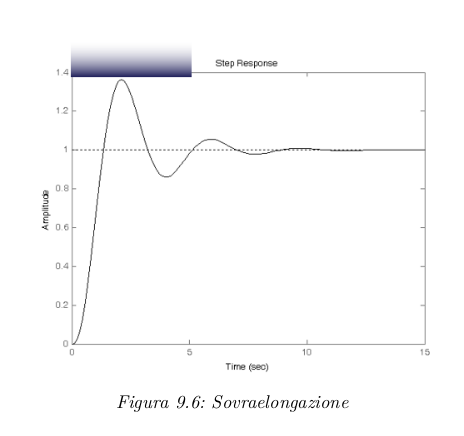
Altre caratteristiche che possono essere oggetto di specifica sono:

• tempo di salita: $t_R=t_{90\%}-t_{10\%}$ (in caso di risposta non oscillante) oppure $t_S=\min (t|y(t_S)=y_{\infty })$ (cioè il primo istante in cui tocca il valore di regime) nel caso di risposta oscillante;
• tempo di assestamento (settling time): $t_a$ necessario perchè $y(t)$ entri in una fascia che si discosti di un massimo noto da $y_{\infty }$.
  

Specifiche sulla risposta in frequenza

Considerando la $F(s)$ del sistema che si sta progettando, si potrebbero avere specifiche sulla sua banda passante e picco di risonanza. Infatti un sistema LTI si può anche vedere come un filtro e opererà correttamente all’interno di un certo range di frequenze.

Specifiche sui disturbi

Vedi IND03.Analisi approfondita delle specifiche di progetto > Disturbi ed effetti su regime permanente.

Specifiche sulla robustezza della stabilità

Vedi IND02b.Uso dei diagrammi e margini di stabilità > Criterio di Nyquist.

Per robustezza si intende la capacità che il sistema ha di rimanere un sistema stabile sebbene il controllore o il sistema reali (realizzati fisicamente) si discostino (per la bontà della fattura o per altri fattori) dal modello teorico, oppure in caso di leggeri discostamenti dovuti a disturbi nei segnali che circolano nel sistema o all’utilizzo improprio del sistema.
Quindi sono indicatori della sensibilità della stabilità del sistema a qualsiasi evento nefasto che possa interessare il sistema stesso.

Scopriremo che indicatori della stabilità del sistema sono da ricercarsi principalmente graficando il comportamento del sistema (la sua risposta) tramite certi strumenti (diagrammi vari e MATLAB) e che esistono legami tra la stabilità della funzione di catena aperta e la stabilità della funzione di catena chiusa.

Specifiche sull’attività sul comando

Spesso si richiede che il comando generato dal controllore non abbia mai, nemmeno nel caso peggiore, modulo troppo alto: infatti un’attività importante del segnale di comando potrebbe causare vari problemi (si prevede spesso che il segnale di comando sia limitato, cappato, vada in saturazione proprio per evitare che si bruci tutto). Esempio, un braccio robotico che si può muovere in diversi mezzi (a contatto con l’aria come immerso nell’acqua) dovrà essere controllato da un controllore che gli dia un segnale di comando più “ampio” in modulo se il braccio incontra la resistenza di un mezzo fluido più denso. Tuttavia, senza un cap, nel caso il braccio robotico incontrasse un fluido troppo denso (o un ostacolo solido) il segnale di comando assumerebbe valori sempre più alti (potenzialmente bruciando tutto) perchè il controllore osserverebbe che la forza attualmente imposta non è abbastanza per muovere il braccio.
Il motore elettrico rischierebbe di fondersi, tipo.