IND05.Discretizzazione di un controllore analogico

Per ora abbiamo sempre considerato il progetto di controllori analogici, quindi la fase successiva al progetto sarebbe la realizzazione, generalmente tramite reti di filtri RLC, di schede elettroniche che implementino le funzioni di trasferimento dei vari componenti del controllore.
Esempio:

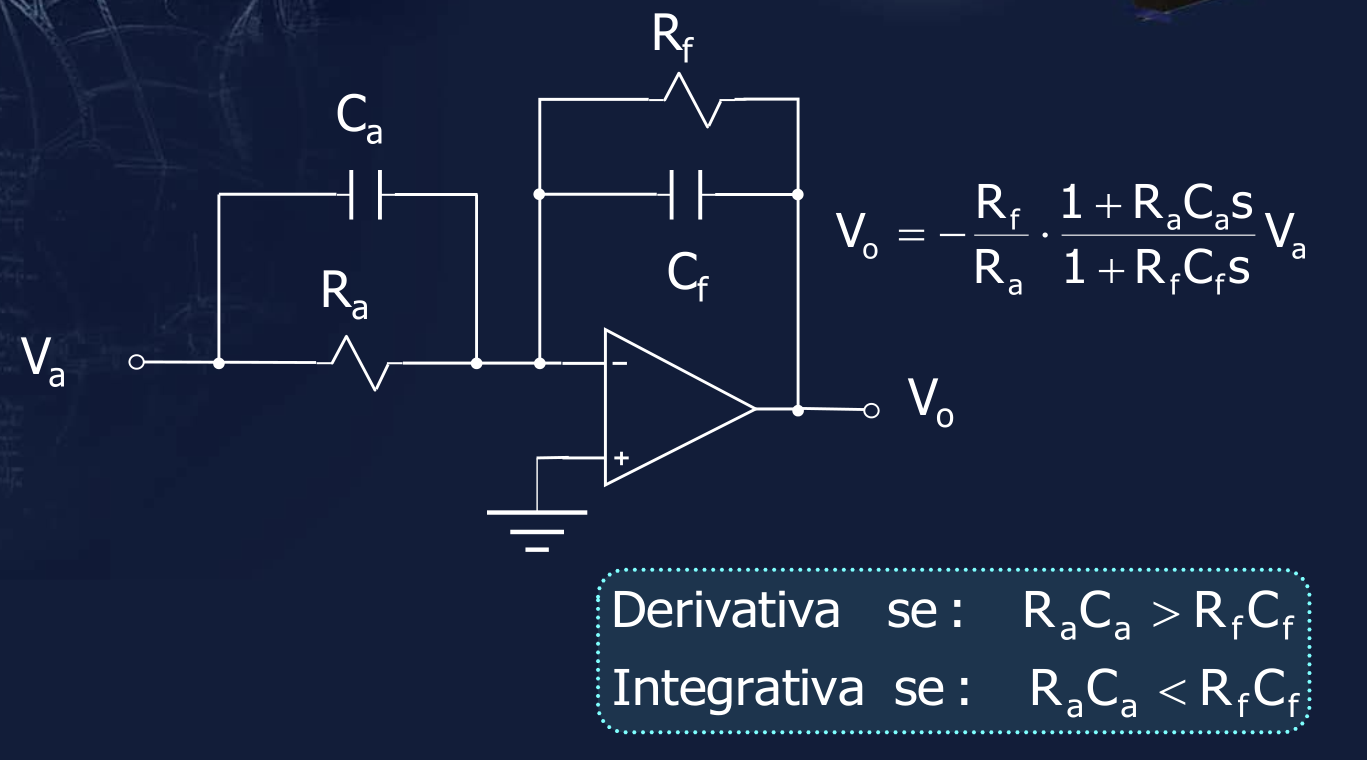
I controllori analogici hanno prestazioni ottimali, tuttavia soffrono di tutti i problemi che caratterizzano una qualsiasi soluzione che venga fisicamente realizzata:

• Degradazione dei componenti (seppur lenta) col passare del tempo
• Incertezza (seppur limitata) nel valore dei parametri (è possibile analizzare la dipendenza delle funzioni di sensibilità della catena chiusa dai vari parametri del controllore)
• Variabilità del valore dei parametri in funzione delle condizioni operative (correnti, pressioni, temperature, ecc.)
• Non linearità (ovvero linearità limitata a un intorno “piccolo” delle condizioni di funzionamento nominali)
• Relativa difficoltà nel “trasportare” e nell’elaborare le variabili in gioco
• Dispendio nel caso si voglia cambiare un parametro del controllore, se non l’intero controllore stesso
• Facilità di generazione e/o captazione di disturbi
  Invece di realizzare dei controllori analogici con componenti “molto stabili” e “molto precisi” (quindi molto costosi) spesso si decide di optare per controllori digitali, che ovviamente risolvono tutti questi problemi, al costo di un po’ di prestazioni e latenza.

Il metodo più semplice di realizzare un controllore digitale consiste nel procedere come già sappiamo al progetto di un controllore analogico, ma poi effettuare una discretizzazione, ovvero campionarne la funzione di trasferimento ed inserire i valori campionati nella memoria di una scheda digitale. Il controllore digitale così ideato dovrà essere posizionato tra un convertitore A/D (per fornire ad esso un’entrata digitale) e un convertitore D/A (in modo che la sua uscita torni ad essere un segnale analogico).

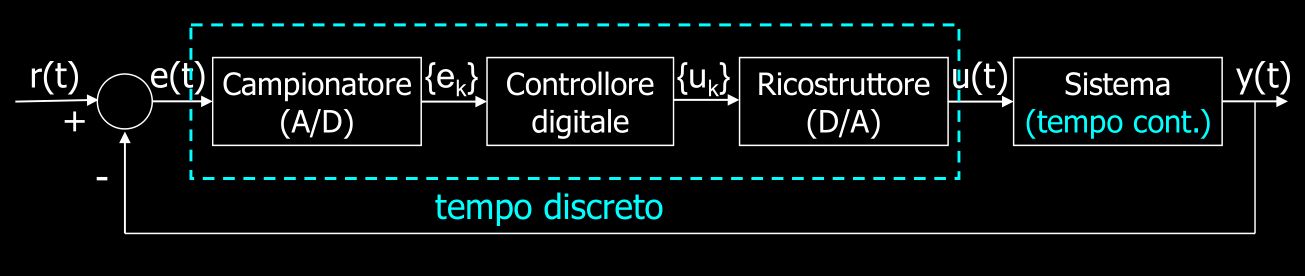
Il campionamento richiede la scelta di un tempo di campionamento adeguato, e successivamente servirà scegliere un metodo di discretizzazione.

Scelta del tempo di campionamento

Per scegliere correttamente il $T_S$ si dovrebbe conoscere la massima frequenza/pulsazione osservabile nello spettro dei segnali con cui il controllore lavorerà, per computare correttamente il minimo di questo parametro tramite il teorema di Shannon.
Tuttavia, di fatto, non conosceremo mai quale sia quella pulsazione; piuttosto opteremo per andare a valutare la ${\omega }_B$ (banda passante della $G_a$ dopo l’inserimento del controllore analogico $C(s)$) e andremo a moltiplicarla per un certo valore $\alpha$.
Dunque
$T_S=\frac{2\pi }{\alpha {\omega }_B}$
Per i problemi elencati sopra, si sceglie $\alpha$ in un intervallo preciso, che per noi andrà sempre bene: $\alpha \in [5,20]$ (e di fatto useremo sempre $\alpha =20$).
Potremo decidere, tuttavia, di ritoccare questo valore in due casi specifici:

• se la perdita di fase dovuta all’inserimento del ricostruttore (quantificabile come vedremo dopo) è talmente alta da causare prestazioni ignobili o addirittura la perdita di stabilità della catena chiusa, si può abbassare $T_S$ per recuperare qualche grado.
• $T_S$ non può fisicamente essere più piccolo di $1$ ms; la tecnologia attuale ci impone questo limite inferiore. Perciò, nel caso in cui la divisione per $\alpha =20$ faccia andare $T_S$ più in basso di $1$ ms sarà necessario alzarlo.

Perdita di fase dovuta ai convertitori A/D e D/A

Il campionatore e il ricostruttore introducono una perdita di fase, data dalle loro funzioni di trasferimento.
Il campionatore in realtà si vede come una moltiplicazione per un treno di impulsi nel tempo, mentre il ricostruttore più utilizzato è quello di tipo Z.O.H. (zero-order-hold: per ogni intervallo di $T_S$ secondi mantiene la sua uscita pari al valore dell’ultimo campione acquisito, quindi ciò che ne esce è una funzione a gradini).
L’effetto sulla fase di entrambi i componenti, supponendo il ricostruttore sia di tipo Z.O.H., è pari all’inserimento di un polo reale stabile in $-T_S/2$.
Per procedere con la discretizzazione di un controllore analogico allora è necessario prima valutare la perdita di fase che viene a ribaltarsi sul margine di fase della catena aperta: una perdita di fase così pronunciata da far crollare il margine di fase sotto gli $0°$ causa l’instabilità del controllore digitale.
Quindi prima di procedere con la discretizzazione sarà sempre necessario computare una nuova $G_a$ che includa il polo introdotto dai convertitori di segnale:
$G_{a,\text{check per discretizzazione}}=\frac{G_a}{1+s\frac{T_S}{2}}$
e valutarne il margine di fase.

Scelta del metodo di discretizzazione

La fase di discretizzazione può seguire vari metodi. Il metodo più comune (che anche MATLAB utilizza di default) è il metodo Z.O.H. (matematicamente equivalente a trasformare in $z$ $C(s)$ in cascata ad un fittizio Z.O.H.).

I metodi disponibili in MATLAB sono:

• Trasformazione Bilineare o di Tustin
• Trasformazione Bilineare con Precompensazione in Frequenza
• Metodo di Invarianza della Risposta al Gradino (matematicamente equivalente a trasformare in $z$ $C(s)$ in cascata ad un fittizio Z.O.H.)
• Metodo della Corrispondenza Poli-Zeri
  E il comando che effettua la discretizzazione è c2d. Non ci interessa davvero sapere cosa questi metodi vanno a fare: ci interessa confrontare il loro output sullo stesso grafico e scegliere il migliore in base a specifiche date oppure in base a criteri auto-imposti.

Discretizzazione in MATLAB

 discretizzazione del sistema  
F1z    = c2d(F1, Ts);  
F2z    = c2d(F2, Ts);  
  
 discretizzazione del controllore   
C_zoh      = c2d(C, 'zoh');  
C_tustin   = c2d(C, 'tustin');  
C_matched  = c2d(C, 'matched');  
C_prewarp  = c2d(C, 'prewarp', wcdes);  
  
%% catene chiuse e plotting  
W_zoh      = feedback(C_zoh     * F1z * F2z, 1/Kr);  
W_tustin   = feedback(C_tustin  * F1z * F2z, 1/Kr);  
W_matched  = feedback(C_matched * F1z * F2z, 1/Kr);  
W_prewarp  = feedback(C_prewarp * F1z * F2z, 1/Kr);  
  
figure();  
hold on;  
stepplot(W_zoh);  
stepplot(W_tustin);  
stepplot(W_matched);  
stepplot(W_prewarp);  
hold off;  
  
% dal confronto tra i tempi di salita / le sovraelongazioni si decide   
% quale sia il miglior metodo di discretizzazione in questo caso