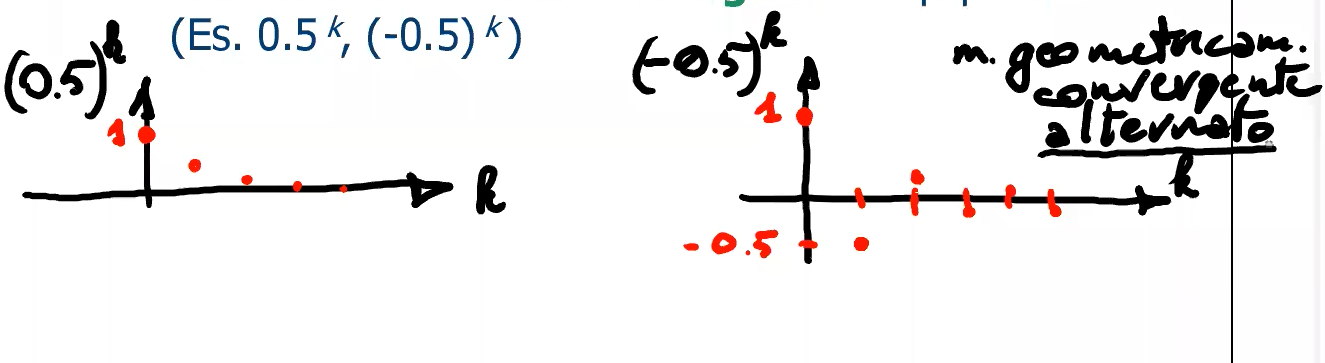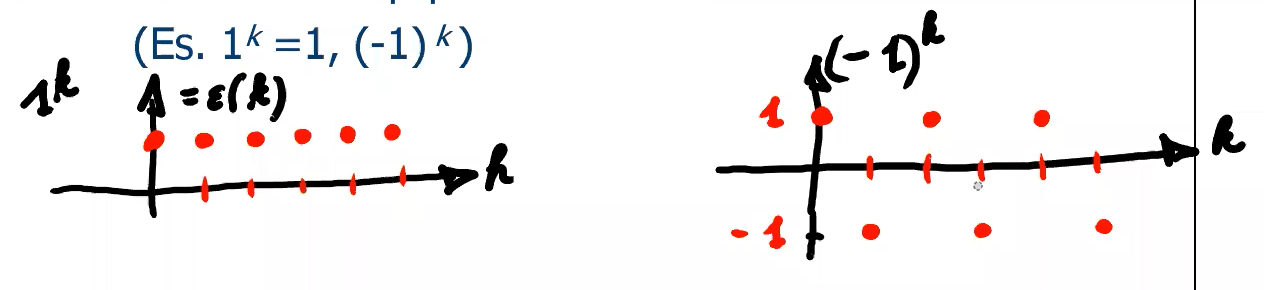TAR11.Analisi modale di sistemi dinamici LTI TD

Recap

• Con l’analisi modale si fa un’analisi qualitativa, della sola evoluzione libera dello stato del sistema, senza dover calcolare interamente l’espressione analitica dell’evoluzione dello stato nel dominio del tempo.
• Tale studio è condotto sulla base dei modi naturali del sistema, in particolare del loro comportamento al tendere del tempo all’infinito.
• La forma dei modi naturali dipende dalla matrice $A$ e in particolare dai suoi autovalori, siano essi reali, coppie complesse coniugate, di molteplicità algebrica unitaria o multipla.

Modi naturali di sistema TD

Anche nei sistemi TD i modi naturali $m(k)$ si possono dire

• convergente se ${\lim }_{k\to \infty }|m(k)|=0$
• limitato se ${\lim }_{k\to \infty }|m(k)|\le M<\infty$
• divergente se ${\lim }_{k\to \infty }|m(k)|=\infty$

In questo caso non c’è di mezzo una matrice esponenziale, perchè non c’è di mezzo la formulazza di Lagrange. Tuttavia, dobbiamo comunque pensare alla formula per scrivere la soluzione direttamente nel dominio del tempo che abbiamo scritto prima, ovvero:
$x(k)=A^{k}x(0)+{\sum }_{i=0}^{k-1}{A}^{k-i-1}Bu(i)=x_l(k)+x_f(k)$
In particolare la parte libera, quindi
$x_l(k)=A^{k}x(0)$
Il calcolo di $A^k$ va fatto ed è immediato solo se $A$ è diagonale, perchè presenta i suoi autovalori sulla diagonale principale e basta elevarli tutti alla $k$.

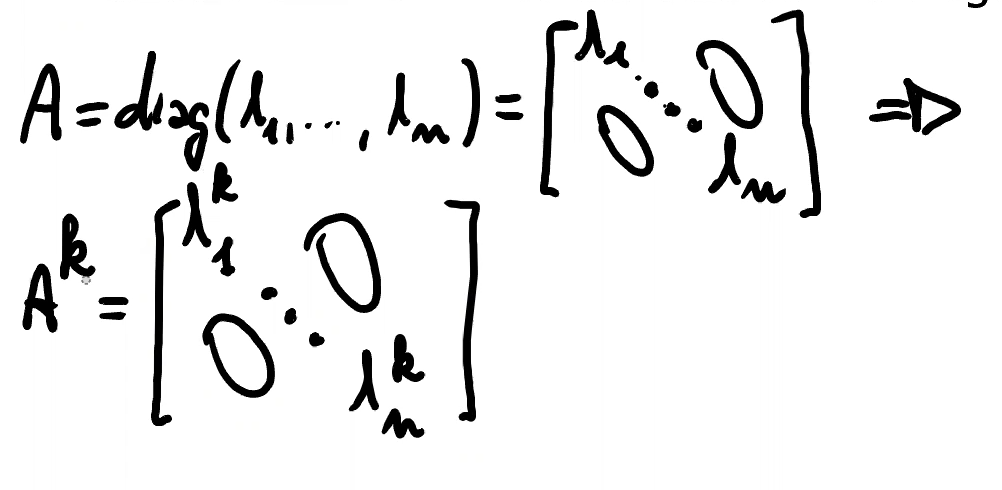
In tutti gli altri casi, ed esattamente come nel caso del TC, ci si deve ricondurre ad una matrice più semplice, in forma di Jordan (diagonale, o diagonale a blocchi), tramite un’operazione di cambio di base / prodotto di similarità che non altera gli autovalori ma semplifica la matrice elevata a potenza.
$A^k=T{\tilde{A}}^k{T}^{-1}$

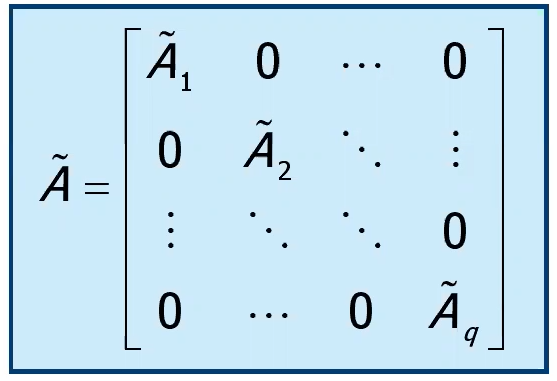
Forme dei blocchi

I blocchi di Jordan sono sottomatrici quadrate associate ognuna ad uno specifico autovalore (o coppia di complessi coniugati) di dimensione ${\mu }_i\times {\mu }_i$, con ${\mu }_i$ molteplicità algebrica dell’autovalore (quante volte annulla il polinomio caratteristico).
La forma dipende dagli autovalori di $A$.

Blocchi corrispondenti ad autovalori reali con molteplicità unitaria

Come nel caso TC: l’intera matrice $\tilde{A}$ sarà una diagonale con gli autovalori sulla diagonale principale, quindi

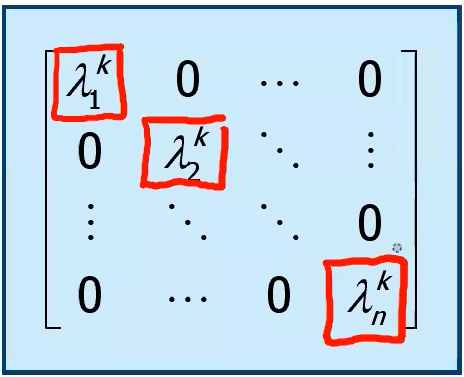
e i modi naturali che ne deriveranno saranno del tipo ${\lambda }_i^k$.
Se $\Re (\lambda )<0$ (la base della potenza) il modo naturale corrispondente sarà alternato, infatti il suo segno è positivo con $k$ pari e negativo con $k$ dispari.

Essi potranno essere classificati ulteriormente come

• geometricamente convergente (alternato o meno): $|\lambda |<1$
  • 
• limitato (alternato o meno): $|\lambda |=1$ (es. $1^k,-1^k$)
  • 
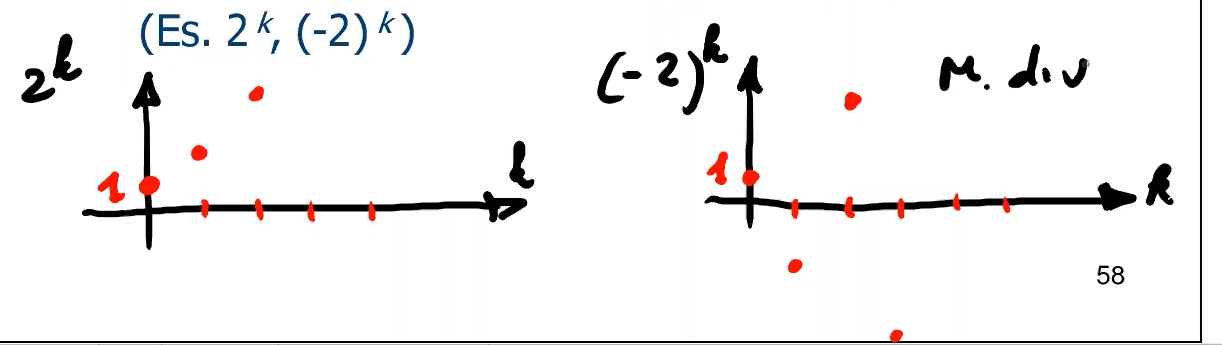
• geometricamente divergente (alternato o meno): $|\lambda |>1$
  • 

Blocchi corrispondenti a coppie di autovalori complessi coniugati con molteplicità unitaria

I blocchi di Jordan corrispondenti a questi, considerando che questi possono scriversi come ${\lambda }_{1,2}=\sigma \pm j\omega =\upsilon e^{\pm j\theta }$
(in effetti, in questo caso bisogna scrivere gli autovalori in forma modulo e fase invece che in forma algebrica)
sono della forma:

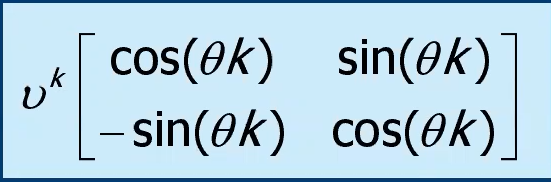
danno origine allora a modi naturali oscillanti del tipo ${\upsilon }^k\cos (\theta k),{\upsilon }^k\sin (\theta k)$
Questi modi si possono classificare come:

• geometricamente convergenti (oscillanti): $\upsilon <1$
• limitati (oscillanti): $\upsilon =1$
• geometricamente divergenti (oscillanti): $\upsilon >1$

Blocchi corrispondenti ad autovalori reali con molteplicità multipla

I blocchi collegati ad autovalori reali con molteplicità algebrica $>1$ sono matrici diagonali a blocchi, i quali blocchi contengono sottomatrici triangolari del tipo:

Danno origine a ${\mu }^{\prime }<\mu$ (${\mu }^{\prime }$ molteplicità geometrica) modi naturali contenenti termini del tipo
$k^{{\mu }^{\prime }-1}{\lambda }^k,...,k{\lambda }^k,{\lambda }^k$
i quali sono classificabili come:

• geometricamente convergenti: $|\lambda |<1$
• polinomialmente divergenti: $|\lambda |=1$
• geometricamente divergenti: $|\lambda |>1$

Blocchi corrispondenti a coppie di autovalori complessi coniugati con molteplicità multipla

I blocchi hanno forma analoga al caso reale.

I modi naturali (in numero ${\mu }^{\prime }<\mu$) che vengono generati sono del tipo:
$k^{{\mu }^{\prime }-1}{\upsilon }^k\cos (\theta k),...,k{\upsilon }^k\cos (\theta k),{\upsilon }^k\cos (\theta k)$
$k^{{\mu }^{\prime }-1}{\upsilon }^k\sin (\theta k),...,k{\upsilon }^k\sin (\theta k),{\upsilon }^k\sin (\theta k)$
Gli inviluppi sono i termini $k^{{\mu }^{\prime }-...}{\upsilon }^k$. I termini sono sicuramente oscillanti.

I modi naturali si possono classificare come:

• geometricamente convergenti (oscillanti): $\upsilon <1$
• polinomialmente divergenti: $|\lambda |=1$
• geometricamente divergenti (oscillanti): $\upsilon >1$