IND03.Regime permanente e transitorio

Posto che ci sia asintotica stabilità, ci siamo garantiti l’esistenza di un regime permanente, in cui il sistema finisce dopo un transitorio.

Precisione in regime permanente

D’ora in poi diciamo inseguimento per dire che abbiamo una $y_{\text{des}}$ e ci aspettiamo che $y$ sia abbastanza simile ad essa, al massimo vari di un errore di inseguimento $e=y_{\text{des}}-y$ usando un riferimento $r$.
Se $r$ è un segnale polinomiale e stiamo usandolo come riferimento vuol dire che stiamo cercando di “inseguire un segnale desiderato” anche esso polinomiale, $y_{\text{des}}=K_{r}r(t)$, al più uguale al riferimento stesso.

Il discorso è: il sistema di controllo agisce su parti del sistema che controlla per regolarne uno stato, che da lui viene stimato tramite informazioni dirette o indirette che ottiene “osservando” il sistema che controlla (direttamente o indirettamente).
Per cui il sistema di controllo di per sè non ha un input e un output nel senso che questo sistema elabora qualcosa. Lui fa solo quello che fa per garantire che lo stato sia regolato. Ed ecco il motivo della retroazione: lui sa che valore deve avere lo stato, perchè tale valore gli viene dato nel riferimento. Lui è forzato dalla retroazione a fare continuamente la differenza tra il valore corrente dello stato e il riferimento. Se la differenza è troppa, il controllore agisce per ristabilire l’equilibrio, e agisce su parti del sistema che controlla. Quindi lui non “produce” nulla di nuovo in output perchè è forzato a produrre lo stesso segnale che gli do in input; non mi serve a niente che lo riproduca. Tuttavia, lui pensa di fare un buon lavoro nel mantenere il segnale uguale all’uscita e pensa che sia quello il suo mestiere. Il suo mestiere è inseguire. Noi glielo facciamo fare perchè “come effetto collaterale” otteniamo delle azioni su un sistema controllato che lo rendono funzionale e funzionante, e a noi è quello che effettivamente serve.

Inseguimento di segnali polinomiali

Se $r(t)=\frac{t^k}{k!}⟹r(s)=\frac{1}{s^{k+1}}$. Se abbiamo un sistema che usa $r$ come riferimento, per capire se è bravo ad inseguire $y_{\text{des}}$, dobbiamo considerare:

• grado di $r(t)$: es. stiamo cercando di inseguire un segnale di grado $2$ = vogliamo ottenere un uscita parabolica
• tipo del sistema: numero di integratori nella FdT in catena chiusa (= numero di poli nell’origine = $h$)
• guadagno stazionario della funzione d’anello / FdT in catena chiusa: ${\lim }_{s\to 0}{s}^{h}G(s)$.
  • se $h=0$ allora il guadagno stazionario $K_G$ è detto guadagno di posizione
    • tipo $1$ di velocità, tipo $2$ di accelerazione
• FdT di $e$: $W_e(s)=\frac{e(s)}{r(s)}=\frac{K_r}{1+G_a(s)}$
  • tramite questa possiamo calcolare il valore a regime di $e(s)$ ovvero $e_{\infty }$ come ${\lim }_{s\to 0}s{W}_e(s)r(s)$
    • 
    • Dalla tabella si nota che:
      • Inseguire un segnale polinomiale di grado $h$ lo puoi fare senza errori in regime permanente solo con sistemi di tipo $>h$.
      • Inseguire un segnale polinomiale di grado $h$ con un sistema di tipo $<h$ è inutile
      • Inseguire un segnale polinomiale di grado $h$ con un sistema di tipo $h$ ti porta ad avere in uscita un errore che si può ridurre aumentando il guadagno della FdT di catena aperta.
      • In definitiva: questo ti serve per capire in base al segnale che vuoi inseguire quanti poli includere nel progetto della funzione di trasferimento della catena chiusa.

Inseguimento di segnali sinusoidali

Se $r(t)=\sin ({\omega }_{0}t)$ (cerchiamo di inseguire un segnale sinusoidale) anche $e(t)$ è sinusoidale e pari a $E\sin ({\omega }_{0}t+{\phi }_e)$ con E=|W_e(j\omega_0)|\implies E_\max=\frac{K_r}{1+G_a(j\omega_0)} e ${\phi }_e=\angle (W_e(j{\omega }_0))$. Non credo serva altro, il resto penso si faccia con MATLAB.

Implicazioni sul progetto del controllore

La precisione dell’inseguimento dell’uscita del sistema rispetto al riferimento in regime permanente è una specifica di progetto. Ad esempio, con un segnale polinomiale e con un indicazione su quanto debba essere $e_{\infty }$ si può già pensare al numero di integratori che si devono avere e al guadagno della catena aperta.

Disturbi ed effetti su regime permanente

I disturbi alla fine sono segnali normali che si sommano a quello che noi trasmettiamo nel sistema.

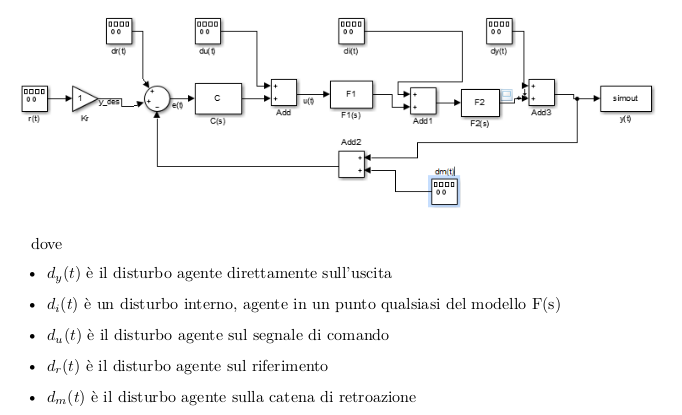
Polinomiali

Disturbo agente direttamente sull’uscita

Disturbo agente sul comando

Esempio completo

Sinusoidali

Esempio completo

Risposta transitoria

Legame tra FdT a catena aperta e a catena chiusa

• La FdT a catena aperta io la chiamo $G_a(s)$
• La FdT a catena chiusa la chiamo $W_y(s)$
• Poi io so che $W_y(s)=\frac{G_a(s)}{1+G_a(s)}$
  • Ma allora gli zeri della catena chiusa sono gli stessi della catena aperta.
    Altre definizioni:
• si dice pulsazione di crossover quella frequenza per la quale il modulo assume valore $0$ dB (la stessa che usavamo per definire il margine di fase).
• si dice “in bassa frequenza” (BF) se si sta parlando di ciò che succede per $\omega <{\omega }_{\text{crossover}}$ per cui $|G_a(s)|\ge 20$ dB (oppure $|G_a(s)|>>1$ in unità naturali)
• si dice “in alta frequenza” (AF) se si sta parlando di ciò che succede per $\omega >{\omega }_{\text{crossover}}$ per cui $|G_a(s)|\le 20$ dB (oppure $|G_a(s)|<<1$ in unità naturali)
• 
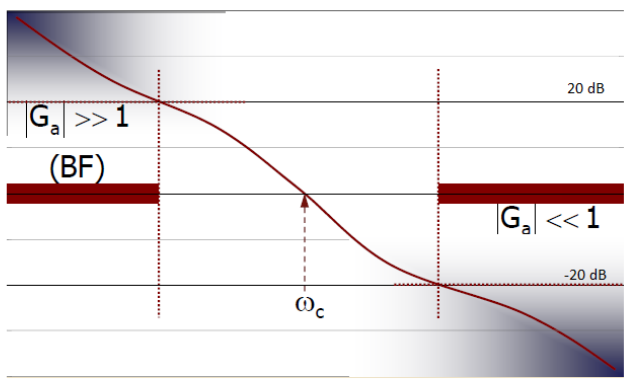
  Si verifica che in BF gli zeri della catena aperta $\approx$ i poli della catena chiusa e in AF i poli della catena aperta sono $\approx$ i poli della catena chiusa.
  Per pulsazioni attorno a ${\omega }_{\text{crossover}}$ (nel transitorio) invece sarà necessario cercare di approssimare con sistemi del secondo ordine il tutto.

Cosa succede in sistemi del secondo ordine?

La FdT in catena chiusa di un sistema del secondo ordine ha espressione
$W_y(s)=\frac{{\omega }_n^2}{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}$ con ${\omega }_n$ e $\zeta$ che sono pulsazione naturale e smorzamento dei due poli complessi che ha questa cosa. (generalmente ti viene dato ${\omega }_n$ e invece $\zeta$ devi assumere sia $\in [0.3,0.7]$ perchè altrimenti avresti picco di risonanza pesante e quindi probabilmente sistema vicino all’instabilità).
Ma è anche vero che $W_y=\frac{G_a}{1+G_a}⟹G_a=\frac{W_y}{1+W_y}=\frac{{\omega }_n^2}{s(s+2\zeta {\omega }_n)}$

Parametri di progetto della $G_a$

Parametri di progetto della $W_y$

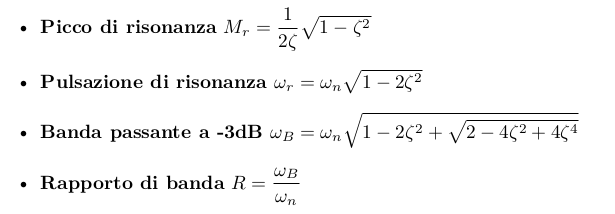
Parametri sulla risposta al gradino

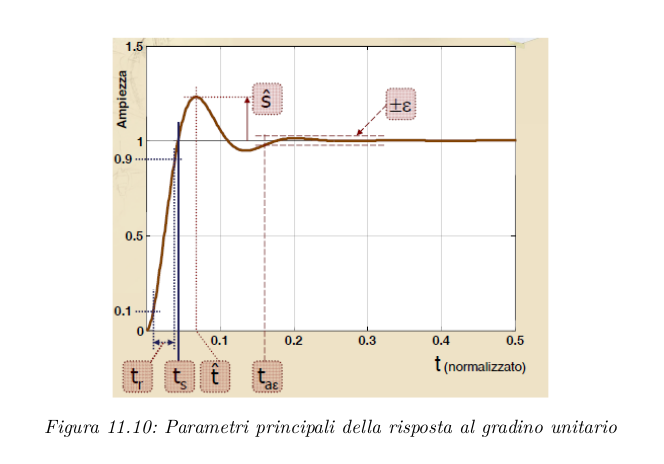
Approssimazioni per questi

Riepilogo

Considerazioni finali sui parametri del transitorio

Insomma, per i parametri del transitorio devi sempre prendere i poli della $W_y$ e costruirci questa $W_{y,\text{approx}}$ che è una FdT di un sistema di secondo ordine, su cui puoi trovarci tutti quei parametri che ti pare e dire quali sono.
L’unico problema è che resta un’approssimazione, per quanto accettabile, quindi c’è un errore $e(t)=|y_{\text{des}}-y(t)|$.

• Si può ridurre l’errore per $0<t<t_s$ riducendo il tempo di salita. Esistendo la relazione ${\omega }_B{t}_s\approx 3$ si potrebbe pensare di aumentare la banda passante, tuttavia questo avrebbe anche effetti su ${\omega }_{\text{crossover}}\approx 0.63{\omega }_B$, che vuol dire che bisognerebbe anche aumentare la pulsazione di crossover.
• Si può ridurre l’errore per $t>t_s$ andando a ridurre la sovraelongazione $\hat{s}$. Esistendo la relazione $1+\hat{s}\approx 0.9M_r$, per ridurre la sovraelongazione si potrebbe pensare di ridurre il picco di risonanza, che a sua volta partecipa in $m_{\phi }{M}_r\approx 60$ qunidi bisogna anche aumentare il margine di fase.
• Non è possibile “ridurre troppo $t_s$ e $\hat{s}$” perchè costa tanto farlo.