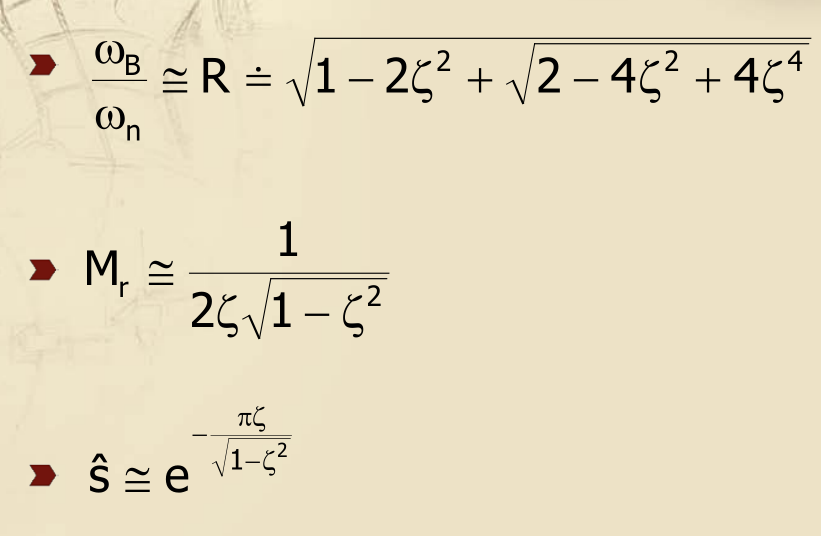IND03.Analisi approfondita delle specifiche di progetto

Precisione in regime permanente

Dato che una specifica inderogabile del controllore è che il sistema, includendo $C(s)$, sia stabile, è possibile sempre parlare di specifiche sul regime permanente. Tuttavia, mentre generalmente parliamo di regime permanente come della risposta al gradino che il sistema produce, qui dobbiamo considerare che lo scopo del sistema in catena chiusa sarà quella di inseguire un riferimento che, in generale, potrebbe non essere un gradino.

Ciò che ci aspettiamo di avere in uscita dal sistema, infatti, è $y=y_{\text{des}}=K_r\cdot r(t)$. Il controllore dovrà allora essere progettato con caratteristiche tali da inseguire correttamente segnali simili ai possibili segnali di riferimento con cui dovrà lavorare.
Per valutare la correttezza dell’inseguimento, si calcola l’errore di inseguimento come $e_{\infty }=y_{\text{des}}-y$.

Warning

La definizione dell’errore d’inseguimento non causa dubbi nel caso generale, in cui l’uscita $y$ è generalmente diversa da $y_{\text{des}}$ perchè attenuata.
In casi più rari, però, il sistema potrebbe produrre un segnale in uscita più alto del segnale di riferimento; in tal caso l’errore di inseguimento esce negativo. Quindi non è impossibile avere un errore di inseguimento negativo; comunque, spesso ci si riferisce all’errore di inseguimento in modulo quindi il problema non si pone.

È quindi comune che nelle specifiche di progetto esistano richieste che specificano quale sia l’errore massimo di inseguimento ammissibile a certe categorie di segnali di riferimento. Inoltre, specifiche del genere possono includere anche richieste sulla reiezione di particolari segnali di disturbo, posizionati in particolari posizioni nello schema del sistema. Anche in questo caso la specifica indicherà il massimo errore di inseguimento ammissibile e la categoria (il grado) del segnale di disturbo da attenuare o reiettare.

Inseguimento di segnali polinomiali

Quando $r(t)$ è un segnale polinomiale (in particolare per noi: un gradino $ϵ(t)$, una rampa $\alpha t$ o un arco di parabola $t^2/2$) l’errore di inseguimento a cui è indotto il sistema è determinato unicamente dal numero di integratori presenti nella catena aperta, ovvero, dal tipo del sistema.
Sistemi di tipo $h$ possono inseguire con errore di inseguimento costante segnali di grado $h$ (positivo o negativo che sia).
Segnali di grado $<h$ saranno inseguiti perfettamente ($|e_{\infty }|=0$), mentre segnali di grado $>h$ non potranno essere inseguiti ($|e_{\infty }|=\infty$).
In particolare, le espressioni che determinano il modulo dell’errore di inseguimento (quando esso è costante) e in assenza di ulteriori disturbi sono:

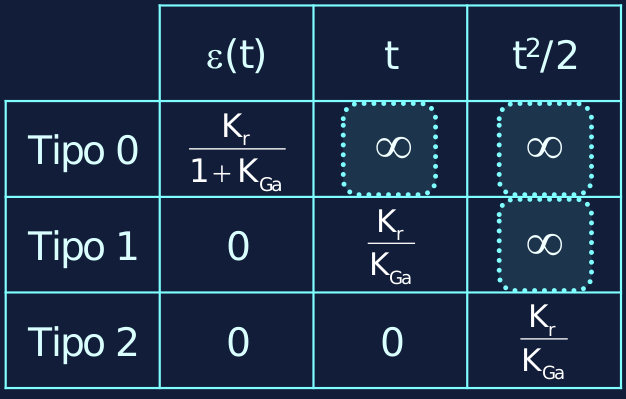
La presenza di $K_{G_a}$ nelle espressioni del modulo dell’errore indicano che specifiche sull’errore di inseguimento a segnali polinomiali si traducono in specifiche sul guadagno statico del controllore $K_C$, dato che $K_{G_a}$ conterrà anche $K_C$.
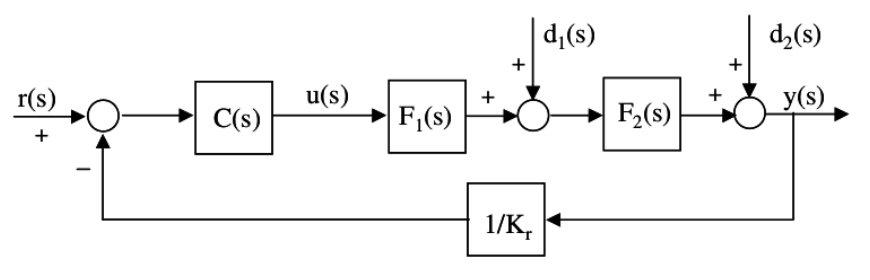
Infatti, in uno schema classico di un sistema controllato, come

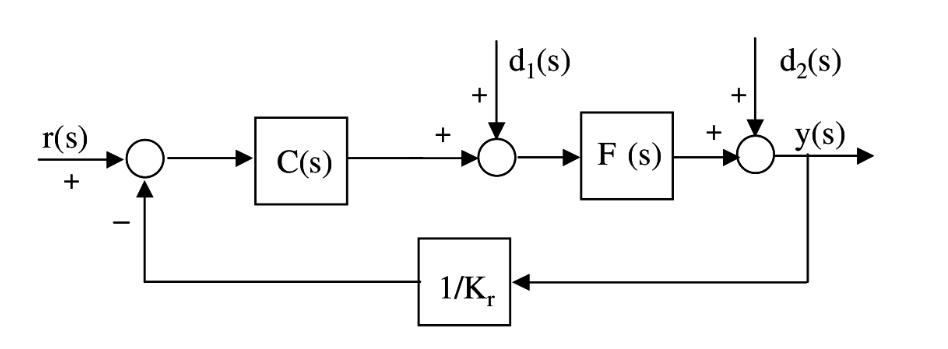
si ha $K_{G_a}=K_C{K}_F/K_r$.

Effetti sull’uscita e reiezione di disturbi polinomiali

I disturbi causano ulteriori errori nell’inseguimento del segnale di riferimento, e anche in questo caso la reiezione o attenuazione di questi segnali, in base alle specifiche, vincola il progetto del controllore nel modulo del guadagno statico del controllore $K_C$ e nel numero di integratori che la catena aperta deve avere (quindi nel numero di fattori del tipo $1/s$ da moltiplicare all’interno di $C(s)$).

A seconda della loro posizione all’interno dello schema e del grado del segnale di disturbo, esso genera un proprio contributo all’errore di inseguimento totale, additivo rispetto all’errore che già il sistema ha nell’inseguire quel particolare grado di segnale di riferimento.
I vari contributi all’errore di inseguimento dovuti a disturbi polinomiali, in modulo, sono:

Warning

Nel nostro solito schema per rappresentare il sistema:

$K_{G_1}$ contiene $K_R$:
$K_{G_1}=K_C{K}_{F_1}/Kr$

Errore di inseguimento totale

L’errore di inseguimento totale resta $e_{\infty }=y_{\text{des}}-y$.
Ogni contributo all’errore totale di inseguimento si inserisce su $y$ additivamente, secondo il principio di sovrapposizione.
In pratica, $y=y_{\text{des}}+e_{\text{dovuto al riferimento}}+e_{\text{dovuto a distubo 1}}+e_{\text{dovuto a distubo 2}}+\dots$
Quindi la formula per il calcolo dell’errore di inseguimento totale contiene un segno $-$:
$e_{\infty ,\text{tot}}=e_{\text{dovuto al riferimento}}-{\sum }_i{e}_{\text{dovuto a disturbo i-esimo}}$

Inseguimento di segnali sinusoidali

Funzione di sensibilità

Effetti sull’uscita e attenuazione di disturbi sinusoidali

Altri parametri di progetto

• Parametri della catena aperta
  • Parametri nel tempo
    • nessuno
  • Parametri in frequenza (letti dal diagramma di Bode della $G_a(s)$)
    • pulsazione di crossover ${\omega }_C$ (a cui il modulo della FdT della catena aperta tocca $0$ dB)
    • margine di fase $m_{\phi }$ (distanza, in positivo, tra la fase della FdT della catena aperta letta in ${\omega }_C$ da $-180°$)
    • margine di guadagno $m_G$ (distanza, in negativo, tra il modulo della FdT della catena aperta letta in ${\omega }_{\pi }$ da $0$ dB)
• Parametri della catena chiusa
  • Parametri nel tempo (letti dal grafico della risposta al gradino della $W(s)$)
    • tempo di salita $t_s\ne t_r$ (primo istante in cui la risposta al gradino tocca il valore finale $y_{\infty }$)
    • sovraelongazione $\hat{s}$ (valore massimo della risposta al gradino della $W(s)$ diviso per il valore iniziale, spesso espresso in percentuale)
    • tempo di picco $\hat{t}$ (istante a cui si ha il valore massimo della risposta al gradino)
  • Parametri in frequenza (letti dal diagramma di Bode della $W(s)$)
    • banda passante ${\omega }_B$ (pulsazione alla quale si ha attenuazione di $-3$ dB nel modulo della $W(s)$ rispetto al valore iniziale $W(0)$)
    • picco di risonanza $M_r$ (valore massimo del modulo della $W(s)$ diviso il valore iniziale $W(0)$)

Lettura dei parametri di progetto in MATLAB

Tips and tricks con MATLAB

• In SIMULINK, la shortcut Ctrl+Shift+L apre la Library Browser. Ctrl+R ruota il componente, Ctrl su un ramo spawna una derivazione del ramo.
• Sempre in SIMULINK, può succedere di dover:
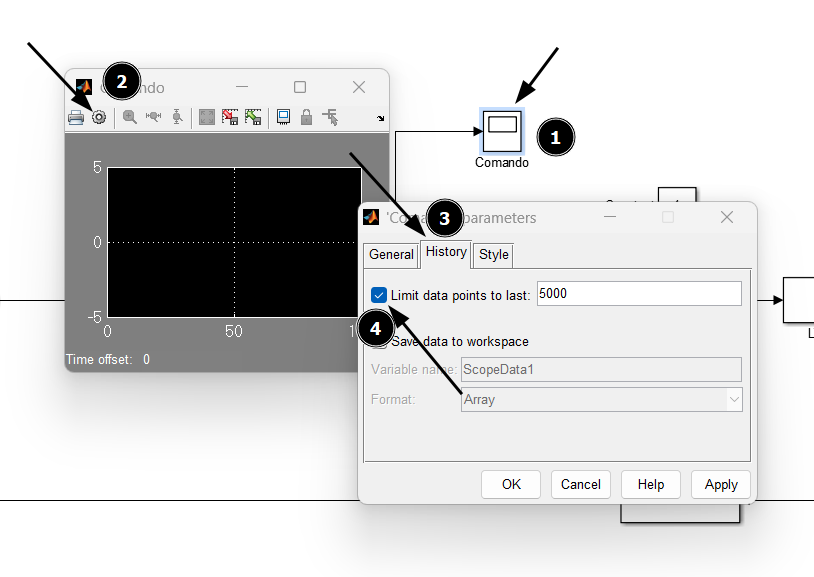
  • dire a MATLAB di non considerare solo gli ultimi 5000 campioni nella visualizzazione degli scope, come normalmente fa, specialmente se si usano tempi di simulazione alti
    • 
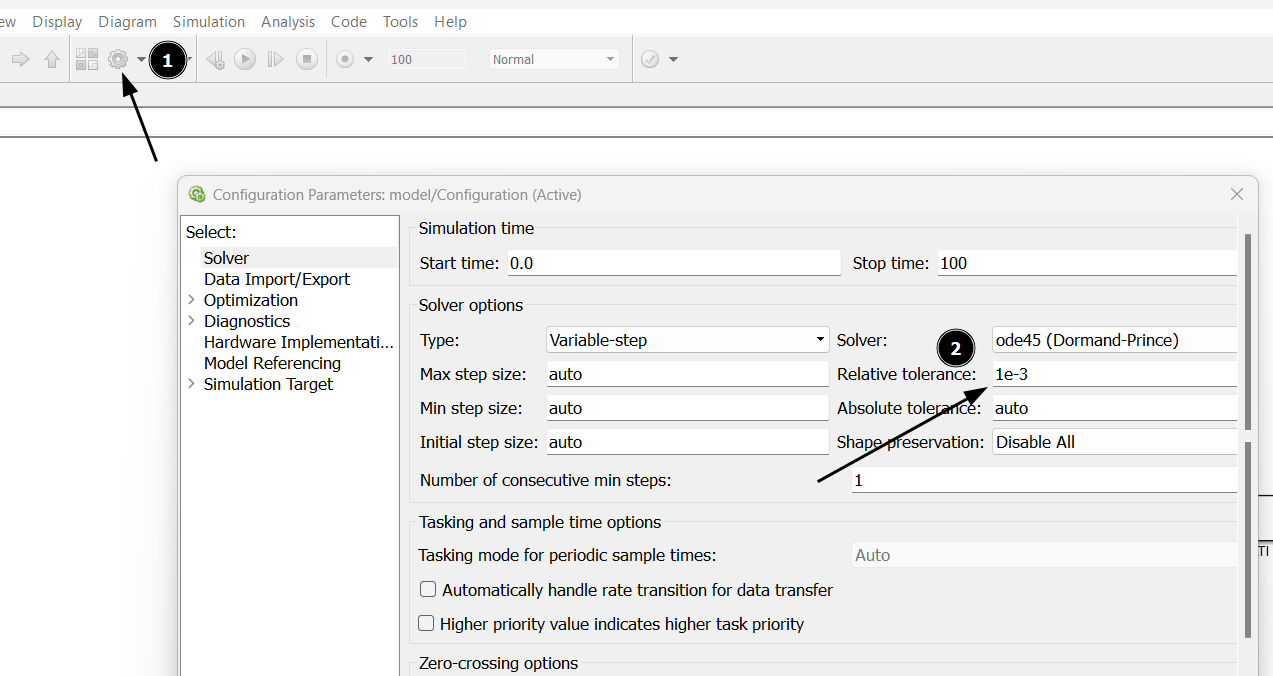
  • dire a MATLAB di usare una tolleranza più bassa in caso si stesse lavorando con segnali di ampiezza molto ridotta (es. dell’ordine di $10^{-}4$)
    • 
• Usare la variante che finisce con -plot dei grafici (bodeplot, nyquistplot, stepplot) ti fa avere opzioni utili con il tasto destro.
• Per selezionare un punto sul grafico per andare a valutarlo, dato che di base MATLAB non metterà il pallino dove clicchi tu ma sul campione più vicino, selezioni lo strumento Tooltip, fai tasto destro > Selection style > Mouse position.
• Stiamo usando MATLAB 2014a.
• Dovendo leggere il valore di un grafico (es. Bode) in una specifica pulsazione, se vuoi farlo comunque manualmente, almeno aiutati mettendo una linea verticale in corrispondenza della pulsazione di interesse (es. line([wcdes, wcdes], ylim)) per vedere immediatamente dove andare a zoomare.
• Il comando [modulo_un, fase] = bode(Ga*C, wcdes) ritorna la lettura del diagramma di Bode in corrispondenza di una pulsazione nota senza bisogno di graficare effettivamente e andare manualmente a vedere. Non va usato sempre perchè se non vedi mai il diagramma di Bode di ciò su cui stai lavorando potresti fare inavvertitamente delle grandi cazzate.
  • la cosa figa, però, è che converte automaticamente il valore del diagramma di Bode del modulo in tale pulsazione in unità naturali, cosa che altrimenti faresti con $10^{x_{dB}/20}$ o con altre funzioni di MATLAB come db2mag.
• la banda passante si può trovare con bandwidth(W).
• la funzione di sensibilità si può scrivere facilmente con sens = feedback(1, Ga)
• per scegliere $m_d$ delle reti derivatrici potrebbe esserti utile scrivere un ciclo

figure();  
hold on;  
for md = 1:10  
	eval(sprintf('Rd_%d = (1 + s) / (1 + s / %d);', md, md))  
	eval(sprintf('bodeplot(Rd_%d);', md));  
end  
hold on;  

Visibili da SIMULINK

Errore di inseguimento

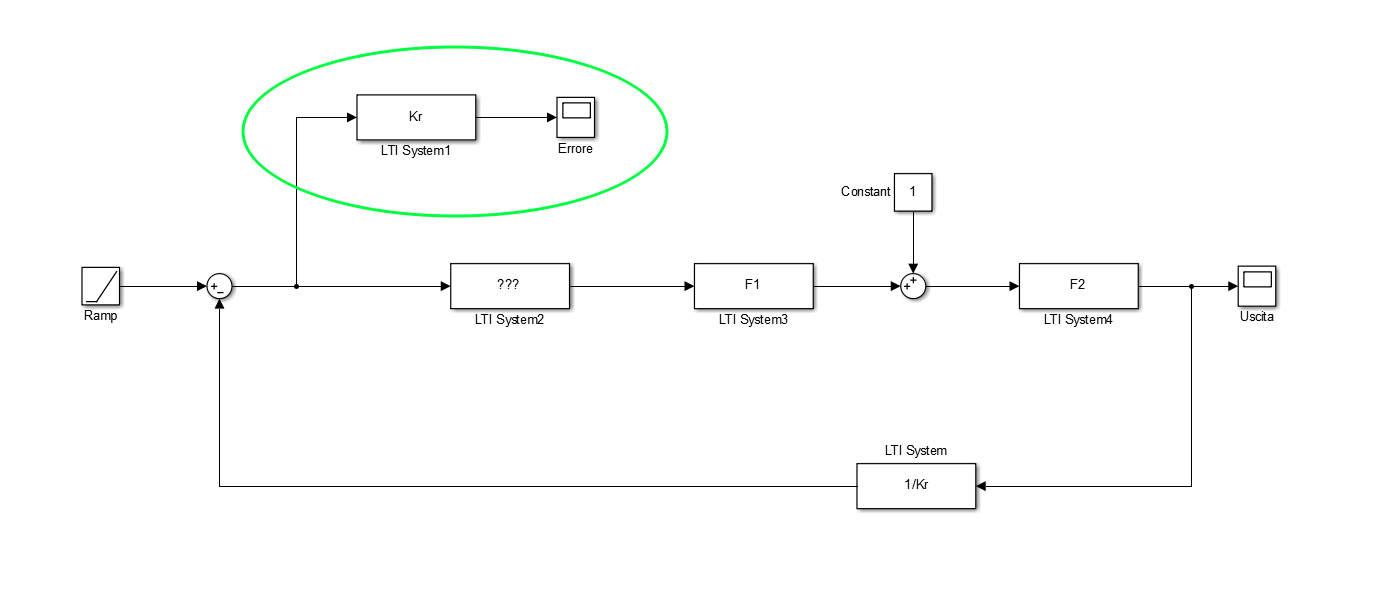
Una volta costruito il modello SIMULINK del sistema in esame, l’errore di inseguimento si può verificare posizionando un sink (tendenzialmente un oscilloscopio) dopo il nodo di differenza che prende in input riferimento e il ramo di retroazione.
Nello schema che normalmente usiamo, tuttavia, bisogna notare che avendo nel ramo di retroazione il blocco di guadagno $1/K_r$ l’errore che leggeremo nello scope posizionato sul ramo uscente dal nodo di differenza è da considerarsi un errore ridotto.
Per leggere l’effettivo valore dell’errore di inseguimento sarà sufficiente moltiplicare questo segnale per $K_r$ prima di portarlo nello scope.

Attività sul comando

Il valore massimo del comando, che sia esso indotto da un disturbo o che si verifichi inseguendo un segnale dato in assenza di disturbi, è da vedersi tramite uno scope collegato all’uscita del controllore.
Il valore massimo del comando è proporzionale a $K_C\cdot \frac{{\prod }_i{m}_{d,i}}{{\prod }_i{m}_{i,i}}$.

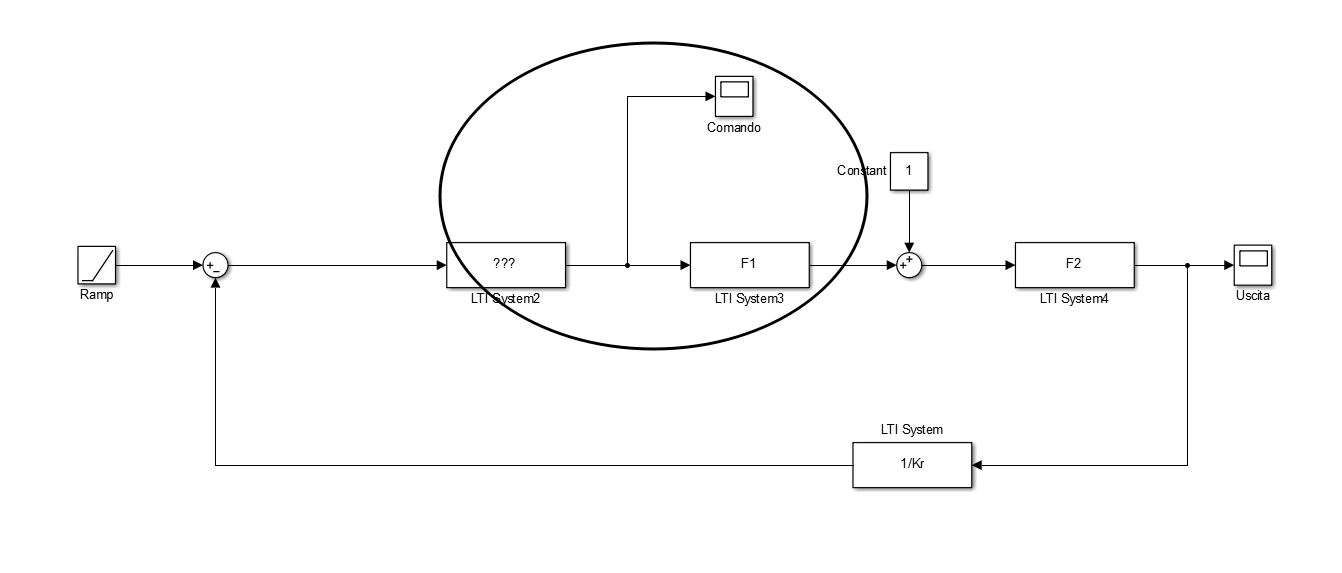
(vabbè, in figura ho lasciato riferimento e disturbi attaccati insieme, tu guarda cosa dice il testo dell’esercizio).

Altri parametri

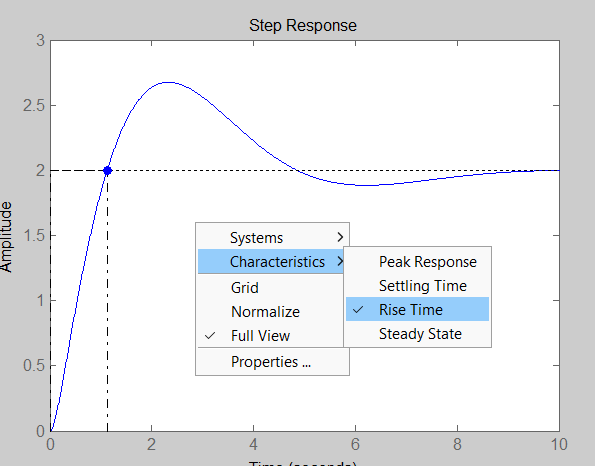
Tempo di salita

Leggibile dalla risposta al gradino. Tuttavia per MATLAB il tempo di salita è sempre quello dal $10\%$ al $90\%$ del valore finale, per cui va prima regolato.
Basta fare stepplot e selezionare tasto destro > Properties > Options e modificare Show rise time between mettendo $0\%$ e $100\%$.
Dopo basta selezionare tasto destro > Characteristics > Rise time.
Se vuoi farlo a mano, basta selezionare il punto in cui per la prima volta il grafico della risposta al gradino tocca il valore di regime.

Sovraelongazione

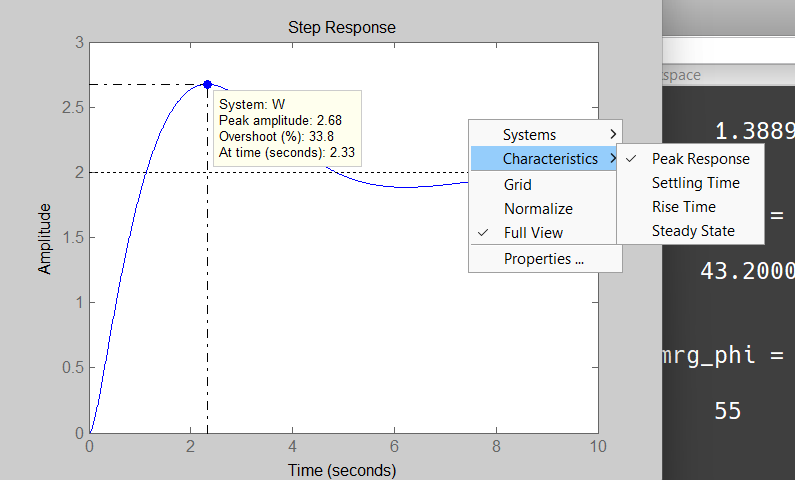
Leggibile dalla risposta al gradino: è sufficiente quindi chiamare figure, stepplot(W), con W=feedback(Ga*Kr, 1/Kr), poi fare tasto destro > Characteristics e selezionare Peak response.
Se volessi invece farlo a mano per una sicurezza ulteriore devi solo cliccare nel punto di massima sovraelongazione (otterrai il picco) e quindi fare (ampiezza del picco $-$ valore iniziale) / valore iniziale.

La funzione di MATLAB da sempre il valore corretto di sovraelongazione (overshoot) in percentuale e anche il valore del picco (occhio: non è il picco di risonanza) (Peak response). Nel caso in cui $K_r$ sia diverso da $1$, perchè l’uscita del sistema inseguirebbe $y_{\text{des}}=K_r\cdot r(t)$, per cui il valore iniziale del gradino sarebbe pari a $K_r$. MATLAB si adatterebbe automaticamente.

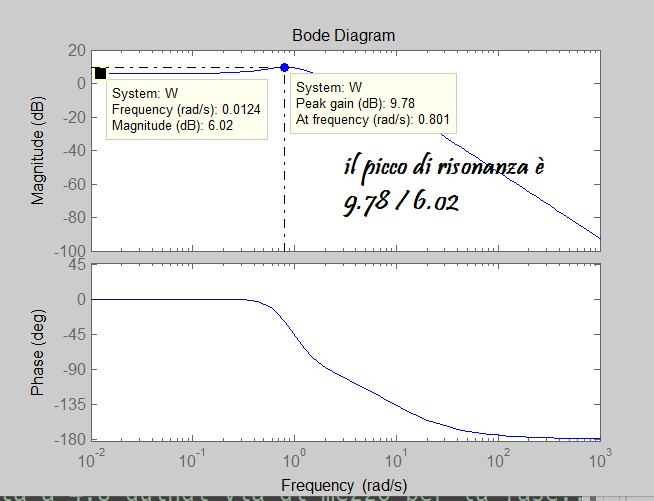
Picco di risonanza

Si vede dal diagramma di Bode. Come nel caso della sovraelongazione, nel caso $K_r$ sia diverso da $1$ bisogna stare attenti, perchè il picco di risonanza è definito come $|\max (W_{dB})/W_{dB}(0)|$, e quindi è un valore relativo al valore iniziale.
Differentemente dal caso della sovraelongazione, il comando Peak response qui ti mostra il Peak gain e non il valore relativo del picco di risonanza. La divisione per il valore iniziale (pari a $K_r$ anche in questo caso, ma in dB) sei costretto a farla a mano.
Alternativa per non sbagliare mai: plotta dividendo per $K_r$ quando devi controllare questa cosa.
Es. figure, bodeplot(W/Kr).

Banda passante

La banda passante è definita come la pulsazione, vista dal diagramma di Bode, alla quale il modulo risulta essere pari al valore iniziale attenuato di $3$ dB. Di conseguenza, anche questo parametro dipende dal valore iniziale e quindi da $K_r$.
Se il valore iniziale è $0$ dB, la pulsazione ${\omega }_B$ è quella a cui il modulo tocca $-3$ dB, altrimenti devi fare la differenza con il valore iniziale ($K_r$ in dB) e vedere quando tocca quella.

Per calcolare la banda passante programmaticamente, esiste il comando bandwidth(W). Ho verificato che funziona anche nel caso $K_r\ne 1$, quindi insomma, win-win.

Relazioni approssimate supponendo comportamento dominante del secondo ordine

C’è anche $m_{\phi }=60-5\cdot M_{r,\text{dB}}$.

Warning

Può tranquillamente succedere che chiudendo la catena con feedback e andando a verificare le specifiche queste non siano rispettate, anche se si sono usate queste relazione correttamente all’inizio dell’esercizio.
Queste relazioni sono approssimate e sono da intendersi tanto più vicine al corretto quanto oiù il sistema è vicino nel suo comportamento a quello di un sistema di secondo ordine.

Per un sistema di secondo ordine, infatti, conosciamo relazioni precise:

e svolgendo i calcoli, queste formulacce si approssimano con i numeri che troviamo, appunto, nelle relazioni che troviamo normalmente.
In tali casi una possibile strada è quella di ri-computare la relazione (ad esempio, saltasse la relazione che lega la pulsazione di crossover alla banda passante, la quale salta spesso con margini di fase molto alti, sarebbe possibili ricomputare la frazione per trovare un valore diverso da $3$ che vada bene, o comunque meglio, e utilizzarlo per calcolare nuovi valori su cui basare i ragionamenti correttivi successivi).

Tipiche richieste di un esercizio di progetto

Un esercizio di progetto di controllore analogico è sempre composto da queste sezioni:

• definizione del sistema (prestare attenzione al valore di $K_r$ e al tipo delle funzioni in gioco)
• specifiche statiche, tipicamente inseguimento di segnali polinomiali in assenza di disturbi e massimo effetto di disturbi polinomiali intermedi al sistema oppure posizionati sull’uscita.
  • Da queste si ricavano informazioni sul valore di $K_C$ (guadagno statico del controllore, tendenzialmente si ottiene sempre quello che è il valore minimo di $K_C$) e sul numero di integratori (poli in $0$) da inserire nel controllore per portare il tipo della catena aperta al minimo possibile valore adatto a reiettare i disturbi e inseguire il riferimento come da specifica.
• specifiche dinamiche, tipicamente range di accettabilità su tempo di salita, banda passante, sovraelongazione massima, picco di risonanza, a volte valore massimo della sensibilità in una certa frequenza.
  • Da queste specifiche si ricavano i due vincoli fondamentali che servono per il progetto del controllore tramite le relazioni approssimate che abbiamo presentato prima.
    • Dalla banda passante si ricava ${\omega }_{C,\text{des}}$ tramite ${\omega }_C=0.63\cdot {\omega }_B$
    • Dal tempo di salita, tramite ${\omega }_B{t}_s\approx 3$, si ritorna ad avere la situazione di sopra
    • Se si avesse una specifica sulla sensibilità ad una certa pulsazione indicata bisognerebbe prendere ${\omega }_C\approx 1.5\cdot {\omega }_{\text{indicata}}$, come valore minimo di ${\omega }_C$.
    • Dal picco di risonanza in dB si ricava il minimo margine di fase, che comunque va confrontato con il minimo di Nichols e va preso il maggiore tra i due, tramite $60-5\cdot M_{r,\text{dB}}$. Invece se si è ottenuto il picco di risonanza massimo in unità naturali si può usare $m_{\phi }\cdot M_r=60$
    • Dalla sovraelongazione si può ricavare il vincolo sul massimo picco di risonanza accettabile tramite $\frac{1+\hat{s}}{0.9}=M_r$ e tornare alla riga sopra.
      Vedremo poi come controbilanciare eventuali problemi nel soddisfacimento delle specifiche dovuti a non idealità che fanno saltare le relazioni approssimate nella loro (già precaria) validità.