IND06.Controllori PID

I controllori PID sono una particolare classe di controllori, molto utilizzati in ambiente industriale perchè non c’è bisogno, per progettarli, di definire un modello completo del sistema da controllare.
Inoltre questi controllori sono completamente definiti da 3 soli parametri liberi, e la taratura (progettazione) di questi parametri può avvenire in maniera algoritmica / automatica.

Questi controllori hanno come scopo quello di arrivare ad avere un regime permanente, quindi di forzare la stabilità della catena chiusa; controllori di questo tipo hanno spesso transitori molto lunghi, ma si è in situazioni in cui i sistemi da controllare sono da accendere una volta e mantenere accesi, quindi

Come tutti i controllori, il loro scopo è di prendere in input l’errore di inseguimento $y_{\text{des}}(t)-y(t)$ e dare in output un $u(t)$ (comando) che diventa l’ingresso del sistema da controllare.
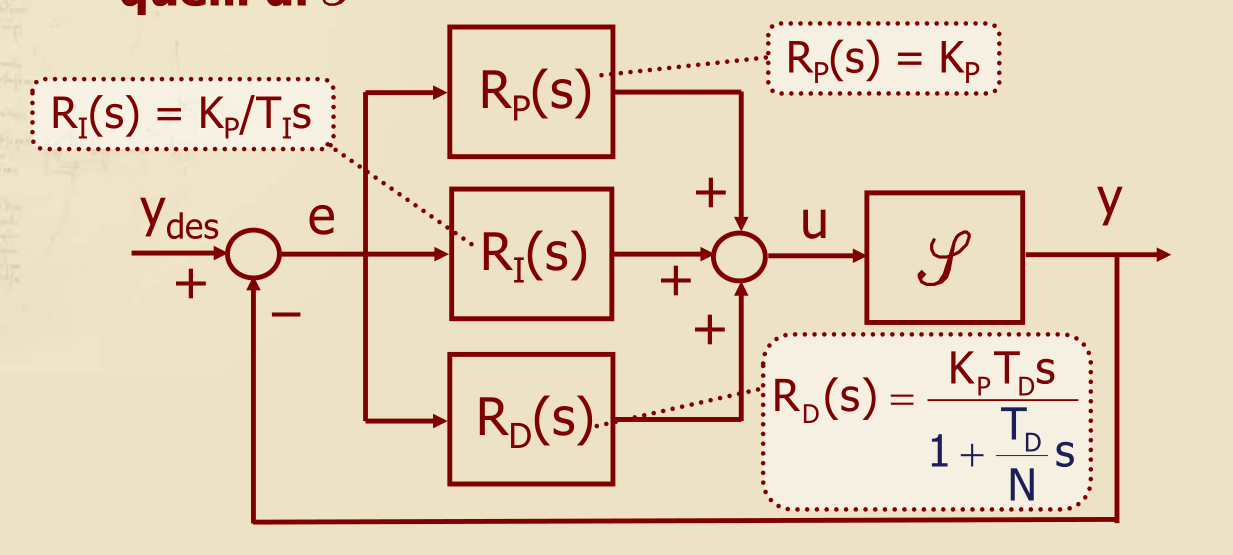
I controllori PID implementano quindi una legge di controllo del tipo $u(t)=K_{P}e(t)+K_I{\int }_{t_0}^{t}e(\tau )d\tau +K_D\frac{d}{dt}e(t)$sono definiti da 3 parti:

• una parte proporzionale all’errore di inseguimento (P), la quale genera un contributo “pronto” e “immediato”, ma che da sola non può garantire l’errore di inseguimento nullo, neppure a segnali di riferimento costanti.
• una parte proporzionale all’integrale dell’errore di inseguimento (I), la quale genera un contributo che tiene conto della storia passata della funzione dell’errore di inseguimento, da un certo istante iniziale $t_0$ fino all’istante corrente
• una parte proporzionale alla derivata dell’errore di inseguimento (D), la quale genera un contributo che cerca di prevedere il futuro movimento della funzione dell’errore di inseguimento.
• se eventualmente non si necessita del contributo di tutte le componenti, si può optare per la costruzione di un controllore P o PI, che quindi contiene solo le prime componenti.

Passando al dominio della frequenza,
$U(s)=K_{p}E(s)+\frac{K_i}{s}E(s)+s{K}_{D}E(s)$
dunque la funzione di trasferimento è
$R_{PID}(s)=K_p+\frac{K_i}{s}+s{K}_D$
spesso, la $R_{PID}(s)$ viene scritta come
$R_{PID}(s)=K_p\left(1+\frac{1}{T_{i}s}+T_{d}s\right)$
$T_i=K_P/K_I,T_D=K_D/K_P$
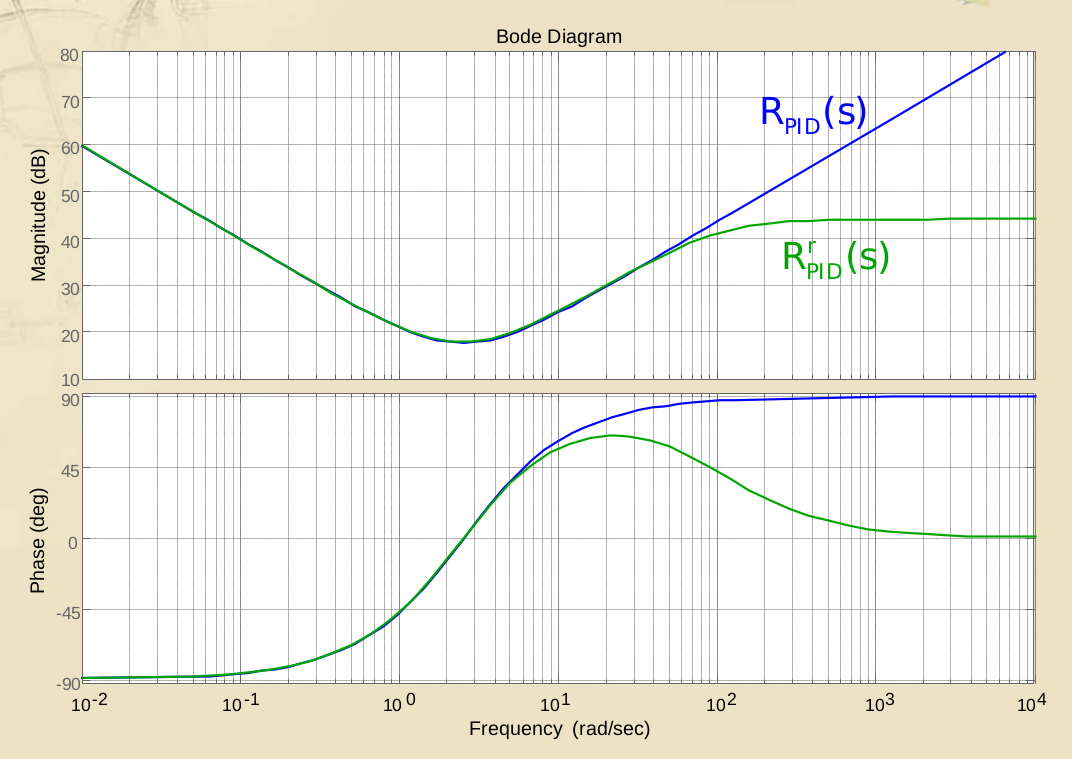
Tuttavia, portando la funzione ad avere un denominatore comune, si nota facilmente come la funzione è impropria: infatti ha due zeri a parte reale negativa ed un solo polo.

Allora questa funzione, essendo impropria, non è fisicamente realizzabile.
È necessario dunque inserire anche un secondo polo, detto di chiusura, $p=-N/T_D$. Idealmente, si dovrebbe cercare di portare questo polo il più possibile in alta frequenza (pulsazione), in modo che gli effetti di tale polo siano nulli o impercettibili alle frequenze di lavoro e siano visibili soltanto intorno ad una pulsazione particolarmente lontana. Quindi un $N\to +\infty$ porterebbe all’idealità.
Però, nella pratica, un $N$ molto grande causa un aumento considerevole dell’attività sul comando. Quindi, valori comuni di $N$ sono tra $5$ e $20$.
La FdT del controllore PID, aggiunto il polo di chiusura, ha la forma:
$R_{PID}^r(s)=K_P\left(1+\frac{1}{T_{i}s}+\frac{T_{D}s}{1+\frac{T_D}{N}s}\right)$

I $3$ parametri che definiscono il PID (quindi tutto tranne $N$, che dovrà essere imposto successivamente) si potranno trovare tramite rapidi calcoli e / o tabelle, detti metodi di taratura.
Esistono metodi di taratura in anello chiuso così come in anello aperto.
Per entrambe le categorie esiste un metodo classico (quello di Ziegler-Nichols), che da in genere risultati poco soddisfacenti dal punto di vista delle prestazioni, anche se la stabilità è solitamente ottenuta, e poi metodi di taratura più avanzati.
Quelli avanzati sono preferibili ogni volta in cui sia necessario garantire migliori indici di robustezza e/o un migliore comportamento del sistema durante il transitorio.

Info

Schemi alternativi
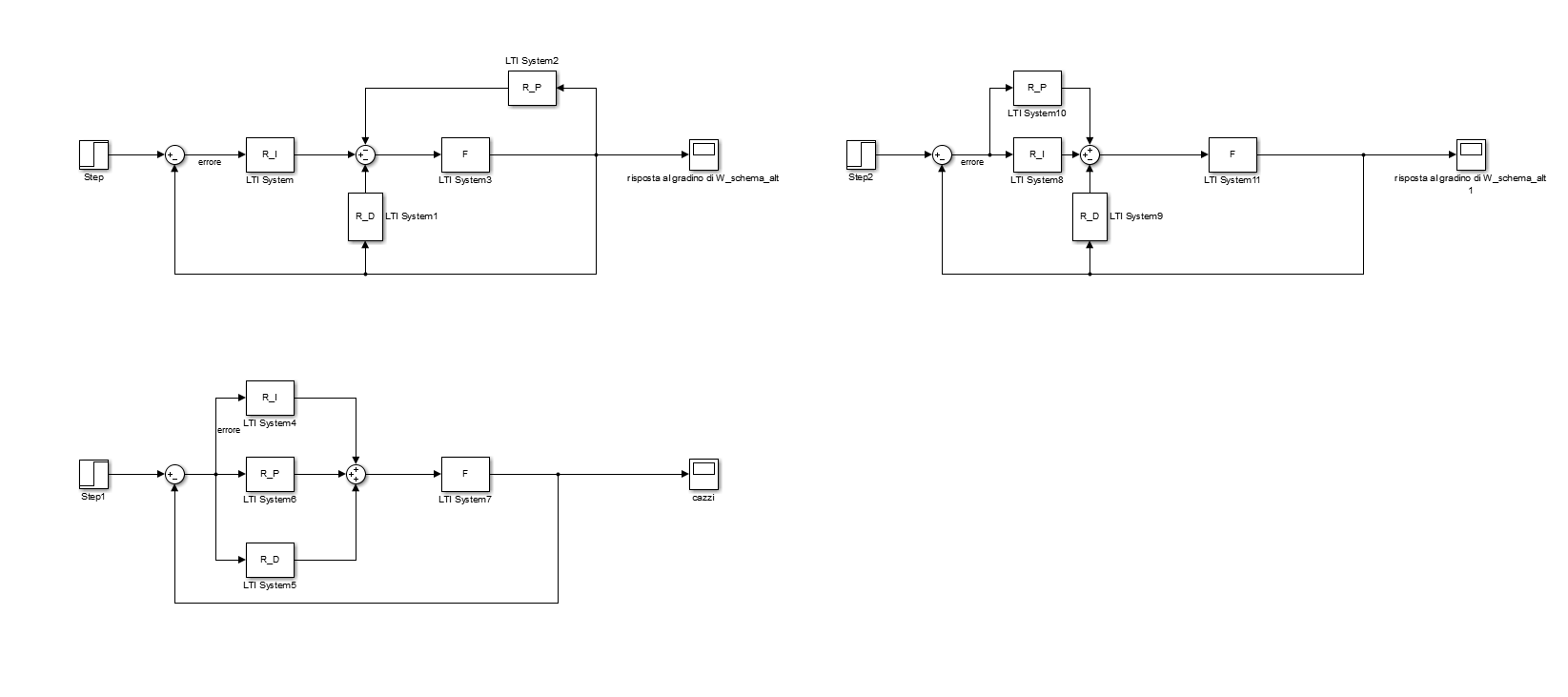
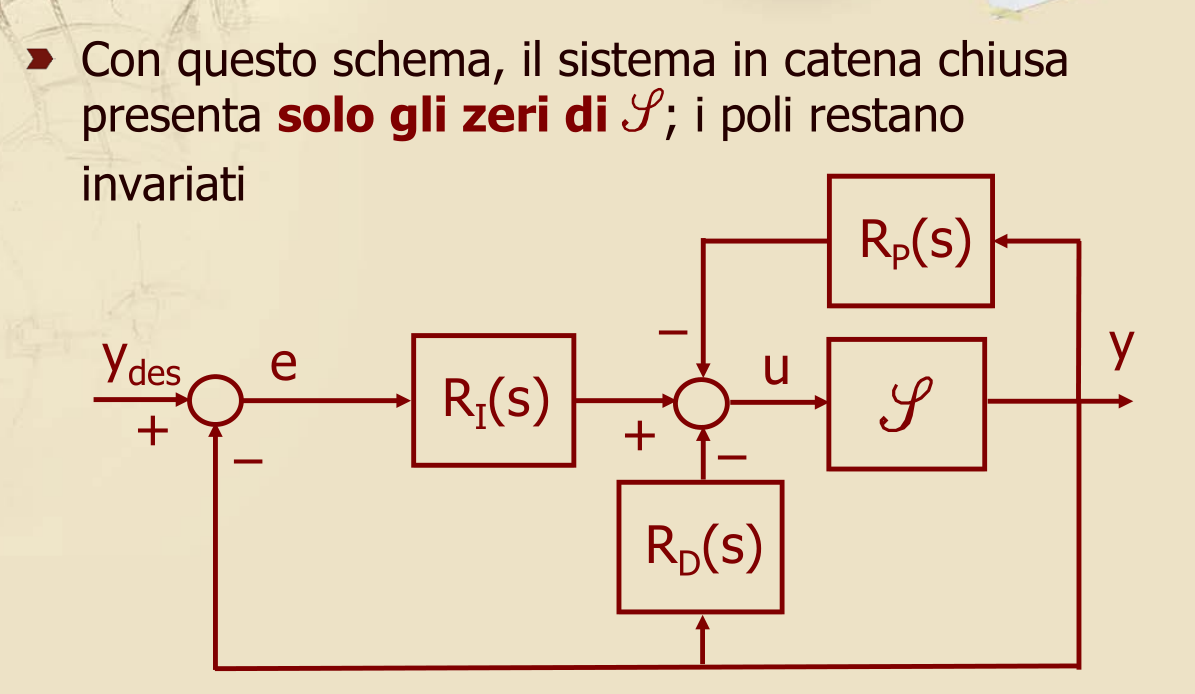
A volte può essere utile, specialmente usando i metodi base di Ziegler-Nichols, procedere con la costruzione dello schema in maniera differente dalli’intuitiva somma dei tre contributi:

Uno schema in cui l’azione di R_D e R_P si ha applicata alla sola uscita è generalmente più lento, ma offre sovraelongazioni più basse e margini di fase maggiori.

Potrebbe convenire provare questo schema dopo aver progettato il PID con Ziegler-Nichols se non si è soddisfatti delle prestazioni e prima di buttare tutto giù e usare i metodi avanzati.

Warning

All’esame
Non ci saranno specifiche sul sistema in catena chiusa dopo l’inserimento del PID progettato: l’unica richiesta sarà garantire la stabilità. Il senso dell’esercizio è più dimostrare di sapere quale famiglia di PID si può costruire.

Metodi di taratura in anello chiuso

Le prove da fare per tarare i parametri sono effettuate retroazionando il sistema con un semplice compensatore statico di guadagno ${\overline{K}}_P$.
Requisiti del sistema perchè siano applicabili i metodi di taratura in anello chiuso:

• il sistema deve avere margine di guadagno finito

Metodo di Ziegler-Nichols in catena chiusa

Il sistema viene posto ai limiti della stabilità; un ulteriore aumento del guadagno lo renderebbe instabile. Infatti ${\overline{K}}_P$ viene preso uguale al margine di guadagno $m_G$ del sistema (va da sè che tale metodo è applicabile soltanto a sistemi aventi margine di guadagno finito - quindi avendo un sistema non a stabilità regolare non si potrebbe usare questo metodo di taratura). Il risultato in uscita da questo sistema così retroazionato presenta un’oscillazione permanente sull’uscita, di periodo $\overline{T}$.
Il periodo $\overline{T}$ dell’oscillazione sull’uscita è pari a $2\pi /{\omega }_{\pi }$.

Una volta ottenuti questi parametri, si calcola la terna caratteristica del PID dalla seguente tabella:

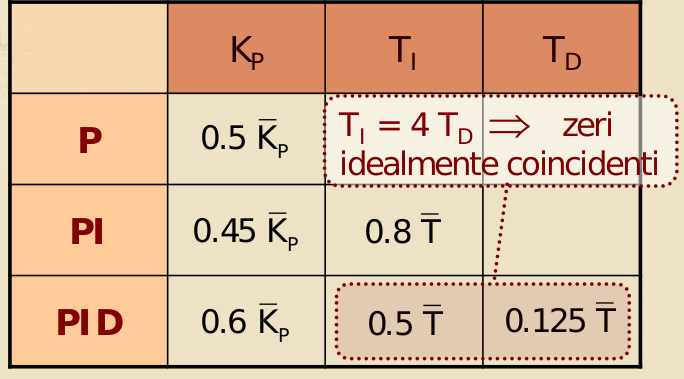
Warning

Un regolatore PID progettato secondo il metodo di Ziegler-Nichols in anello chiuso fornisce solitamente un margine di fase inferiore a $40°$.
La risposta al gradino del sistema controllato presenta oscillazioni poco smorzate.

Metodo di imposizione del margine di fase

Se risulta accettabile imporre che ${\omega }_C={\omega }_{\pi }$, allora è possibile assegnare un margine di fase desiderato imponendo

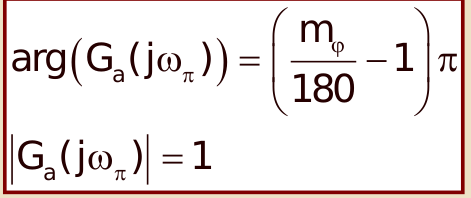
ove $G_a(j\omega )$, non nota, è la fdt d’anello risultante dall’inserimento del regolatore PID.
Si ottengono allora le seguenti relazioni:

Metodi di taratura in anello aperto

Le prove da fare per tarare i parametri sono effettuate direttamente sul sistema ancora aperto e senza alcun tipo di controllo inserito.
I metodi di taratura in anello aperto sono basati sulla determinazione di un modello approssimato del processo da controllare, a partire dalla risposta del sistema ad un riferimento noto (gradino).

Requisiti del sistema perchè siano applicabili i metodi di taratura in anello aperto:

• il sistema deve avere regime permanente (essere asintoticamente stabile già in catena aperta)
• avere risposta al gradino monotona (non presentare sovraelongazione)

Non è importante che il sistema sia di un certo ordine; generalmente si guarda la risposta al gradino e si adatta un’approssimazione del primo ordine, in modo che siano abbastanza simili la funzione approssimata e la reale risposta al gradino.

Metodo della tangente

Si utilizza una FdT approssimata del I ordine con ritardo:
$F(s)=\frac{K_F}{1+{\tau }_{F}s}{e}^{-{\theta }_{F}s}$
I parametri $K_F$, ${\tau }_F$ e ${\theta }_F$ si possono vedere dal grafico della risposta al gradino:

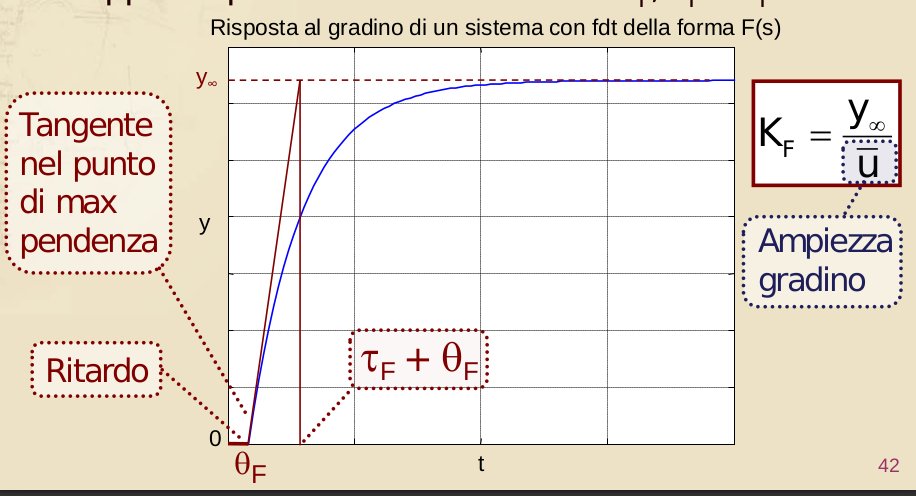
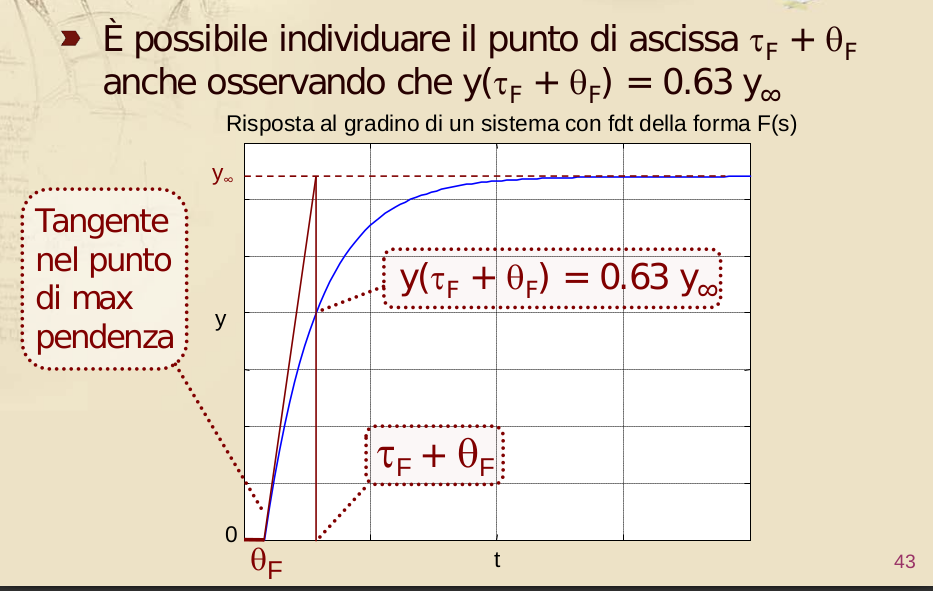
Metodo di Ziegler-Nichols in catena aperta

Una volta trovati questi parametri col metodo della tangente, si può calcolare la terna caratteristica del PID tramite la seguente tabella (metodo di Ziegler-Nichols in catena aperta):

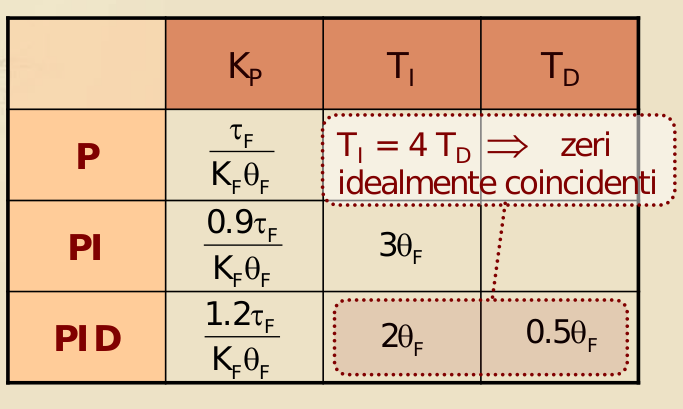
Warning

Anche in questo caso si ottiene un margine di fase non grande.

Metodo di Cohen-Coon

Questa tabella è stata determinata imponendo un rapporto di smorzamento pari a $0.25$ tra due picchi consecutivi della risposta del sistema al gradino sul comando $u$.

Metodo IMC (Internal Model Control)

Non ho voglia di scrivere che cosa vuol dire sto coso, ma la tabella è questa.

Warning

Il parametro aggiuntivo $T_f>0$ permette di agire sulla banda passante e sui margini di stabilità: all’aumentare di $T_f$, ${\omega }_B$ diminuisce ed i margini di stabilità (sia $m_G$ che $m_{\phi }$) aumentano.

Esempio con MATLAB

 definizione sistema  
s       = tf('s');  
F       = ( 5*(1+s/4) )/( ((1+s)^2)*((1+s/16)^2) );  
  
pole(F)  
zero(F)  
 Ziegler-Nichols  
[Gm, Pm, wpi, wc]  = margin(F)  
Kpsegnato   = Gm  
Tsegnato    = 2*pi/(wpi);  
% ora uso la tabella  
Kp  = 0.6   * Kpsegnato;  
Ti  = 0.5   * Tsegnato;  
Td  = 0.125 * Tsegnato;  
N   = 20;  
  
% calcolo la funzione di trasferimento del PID  
R_P     = Kp;  
R_I     = Kp/(Ti*s);  
R_D     = Kp*s/(1+Td/N*s);  
R_PID   = R_P+R_I+R_D;  
  
% controllo il margine di fase ottenuto  
Ga_PID_ZN = R_PID * F;  
figure, margin(Ga_PID_ZN);  
  
% chiudo   
figure, stepplot(feedback(Ga_PID_ZN, 1));  
  
% controllo uno schema alternativo  
% % è migliore, guadagno di abbassarci sovraelongazione e ts.  
  
%% metodo avanzato (da fare, volendo, anche se all'esame non ci saranno specifiche e quindi probabilmente mi basterà fare Z-N)