TAR06.Analisi nel dominio del tempo e della trasformata di Laplace di sistemi LTI TC

Soluzione nel dominio del tempo

Il comportamento dinamico di un sistema LTI TC a dimensione finita è descritto dalle equazioni di ingresso-stato-uscita
$\dot{x}(t)=Ax(t)+Bu(t)$
$y(t)=Cx(t)+Du(t)$
dove:

• $x$ è il vettore colonna delle variabili di stato e ha $n$ righe
• $u$ è il vettore colonna degli ingressi e ha $p$ righe
• $y$ è il vettore colonna delle variabili di interesse e ha $q$ righe
  di conseguenza:
• $A$ è una matrice quadrata $n\times n$
• $B$ è una matrice rettangolare $n\times p$
• $C$ è una matrice rettangolare $q\times n$
• $D$ è una matrice rettangolare $q\times p$
  A partire da uno stato iniziale $x(t=0_{-})$ noto e conoscendo le matrici $A$ e $B$, e $u(t)$ si dovrà quindi, per conoscere l’evoluzione del sistema nel tempo, risolvere la prima equazione differenziale in modo da trovare $x(t)$ (il movimento dello stato). Una volta trovato quello dalla prima equazione (che serve solo a quello) si può sostituire nell’equazione delle uscite e ottenere un’associazione input-output.
  L’espressione di $x(t)$ si calcola con la formula di Lagrange (che è un casino inutile da scrivere e non si usa negli esercizi) - l’importante è che la soluzione dipende da due parti:
  
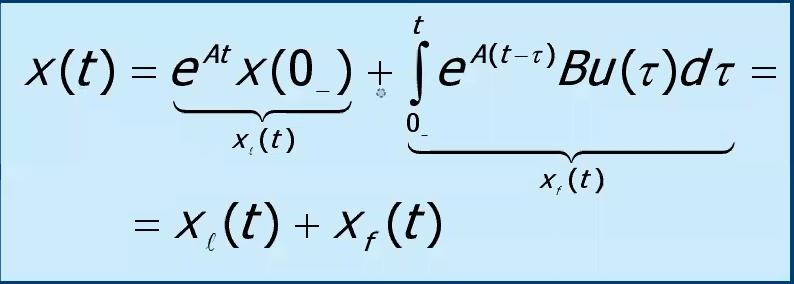
• il primo contributo dipende solo dallo stato iniziale $x(0_{-})$, ovvero dall’equazione omogenea associata all’equazione differenziale
  • $\dot{x}(t)=Ax(t)$
• Questo contributo è detto movimento libero dello stato.
• il secondo contributo (movimento forzato dello stato) è invece un prodotto di convoluzione che dipende dall’ingresso e non dallo stato iniziale.
  L’andamento di $y(t)$, detto movimento dell’uscita, si ottiene dalla sua relazione statica sostituendo per $x(t)$ l’espressione data dalla formula di Lagrange. Anche l’uscita, quindi, è la somma di una risposta libera e di una risposta forzata.
  Il problema principale di questo calcolo è la matrice esponenziale $e^{At}$, che è una matrice con le stesse dimensioni della matrice $A$, ma è una matrice di funzioni nel tempo che non abbiamo davvero voglia di fare, perciò cercheremo vie alternative. E poi c’è un bruttissimo prodotto di convoluzione a destra.

Soluzione nel dominio di Laplace

Questo lo facciamo negli esercizi. La trasformata che usiamo per questo corso è la trasformata unilatera di Laplace, ovvero:
$F(s)=\mathcal{L}\{f(t)\}={\int }_{0_{-}}^{+\infty }f(t)e^{-st}dt$
(si usa $0_{-}$ per evitare problemi di definizione dell’integrale nel caso di funzioni discontinue in $0$). Le proprietà sono le solite:

• linearità (trasformata di combinazione lineare = combinazione lineare di trasformate)
• $\mathcal{L}\{\dot{f}(t)\}=sF(s)-f(0_{-})$
• $\mathcal{L}\{\ddot{f}(t)\}=s^{2}F(s)-sf(0_{-})-\dot{f}(0_{-})$
• $\mathcal{L}\{{\int }_{0_{-}}^{t}f(\tau )d\tau \}=\frac{F(s)}{s}$ (sembra quasi il reciproco della trasormata della derivata, ma nessuna dipendenza da $f(0_{-})$)
• $\mathcal{L}\{f(t-\tau )\}=F(s)e^{-\tau s},e^{-s\tau }\in \mathbb{C}$
• $\mathcal{L}\{f_1(t)\ast f_2(t)\}=F_1(s)F_2(s)$
• tabella delle trasformate utili:
  • 
    Esempio:
    segnale a rampa unitaria: integrale nel tempo del segnale $ϵ(t)$. La sua trasformata di Laplace è quindi $\frac{1}{s}$ per la trasformata del gradino. (quindi $\frac{1}{s^2}$).

Tutti i segnali che analizziamo sono unilateri (diversi da $0$ da $t=0_{-}$ in poi). Quindi conviene dire che tutti i segnali sono moltiplicati per il gradino $ϵ(t)$.

$\frac{t^n}{n!}$ è il cosiddetto segnale polinomiale.

In $e^{at}$, $a$ può essere $\in \mathbb{C}$.

La trasformata della matrice esponenziale è una matrice quadrata di espressione $(s{I}_n-A{)}^{-1}$, con $I_n$ la matrice identità di dimensioni $n\times n$.

Soluzione nel dominio della frequenza

• Si applica la trasformata di Laplace alle equazioni dello stato nel dominio del tempo
  • $\mathcal{L}[\dot{x}(t)]=\mathcal{L}[Ax(t)+Bu(t)]$
• Lavorandoci si ottengono la trasformata di Laplace dei movimenti dello stato e di uscita (porto a primo membro tutti i termini che dipendono da $X(s)$, ricordando che il prodotto matriciale non è commutativo - se trovi una somma tra scalare e matrice, moltiplica per $I_n$ lo scalare). Poi puoi dividere per una matrice (ovvero moltiplicare per l’inversa, se esiste).
  • L’inversa esiste se il determinante $\ne 0$
  • Il determinante di $(s{I}_n-A)$ è un polinomio in $s$ di grado $n$ a coefficienti reali
  • Il polinomio è non nullo in tutti i punti tranne che in $n$ radici, dette autovalori; l’inversa quindi esiste (e di conse guenza la soluzione esiste) per tutti i valori di $s$ tranne che per gli autovalori.
• Si nota il legame tra la formula di Lagrange e l’espressione di $X(s)$ trovata. Ai due contributi sono semplicemente sostituite le loro trasformate di Laplace.
• Si ottengono allora i movimenti nel dominio del tempo applicando una anti-trasformata alle equazioni trovate.
  $\dot{x}(t)=Ax(t)+Bu(t)=\frac{dx(t)}{dt}$
  $\mathcal{L}\{\dot{x}(t)\}(s)=\mathcal{L}\{Ax(t)+Bu(t)\}=\mathcal{L}\left\{\frac{dx(t)}{dt}\right\}$
  Dalle proprietà di linearità e di derivazione nel tempo della TdL:
  $AX(s)+BU(s)=sX(s)-x(0^{-})$
  $BU(s)+x(0^{-})=sX(s)-AX(s)$
  $BU(s)+x(0^{-})=(sI-A)X(s)$
  $(sI-A{)}^{-1}BU(s)+(sI-A{)}^{-1}x(0^{-})=$
  $=(sI-A{)}^{-1}(sI-A)X(s)$
  Da cui
  $X(s)=(sI-A{)}^{-1}x(0^{-})+(sI-A{)}^{-1}BU(s)=$
  $=X_l(s)+X_f(s)$
  Facendo la trasformata di Laplace di ambo i membri dell’equazione dell’uscita $y$ e sostituendoci la $X(s)$ trovata dal procedimento precedente si trova:
  $y(t)=Cx(t)+Du(t)$
  $Y(s)=CX(s)+DU(s)$
  $Y(s)=C[(s{I}_n-A{)}^{-1}{x}_{0_{-}}+(s{I}_n-A{)}^{-1}BU(s)]+DU(s)$
  $Y(s)=C(s{I}_n-A{)}^{-1}{x}_{0_{-}}+[C(s{I}_n-A{)}^{-1}B+D]U(s)$
  $Y(s)=C[(s{I}_n-A{)}^{-1}{x}_{0_{-}}+(s{I}_n-A{)}^{-1}BU(s)]+DU(s)$
  $Y(s)=H_0{x}_{0_{-}}+H(s)U(s)$
  Con $H(s)$ che è la matrice di trasferimento del sistema. Questa funzione può, da sola, rappresentare l’intero sistema, a patto che si parta da $x_{0_{-}}=0$, ovvero che nell’istante iniziale il sistema si possa considerare “a riposo”.

Info

Le due rappresentazioni del sistema LTI (tramite rappresentazione in variabili di stato / eventualmente matriciale e tramite la sola funzione di trasferimento) non sono in generale equivalenti.
Esse sono equivalenti, in generale, solo se supponiamo che il sistema si muova da $x_0=\vec{0}$, ovvero che tutte le variabili di stato siano inizialmente a valore nullo. Quello che ne deriva è che consideriamo unicamente la risposta forzata del sistema, che dipende solo dagli ingressi e non la risposta libera, che appunto dipende dallo stato iniziale (decidiamo deliberatamente di ignorarla, magari perchè non rilevante in termini di intensità rispetto alla risposta forzata).

C’è anche un caso in cui le rappresentazioni sono equivalenti a prescindere e interscambiabili, ovvero il caso in cui la risposta del sistema è veramente solo la risposta forzata: quando il sistema è in forma minima.

In tal caso è possibile anche passare dalla rappresentazione in FdT ad una (una delle possibili) realizzazioni di tale FdT (quindi ad un sistema che la implementi, scritto come rappresentazione in variabili di stato / eventualmente matriciale) senza perdita di alcuna informazione sul sistema. Esempi dal futuro su come ricavare una realizzazione da una FdT: Realizzazione 1, Realizzazione 2

Questa funzione $H(s)$ è, in generale, una matrice complessa rettangolare $p\times q$, i cui elementi sono rapporti di polinomi (= funzioni razionali fratte) nella variabile complessa $s$.

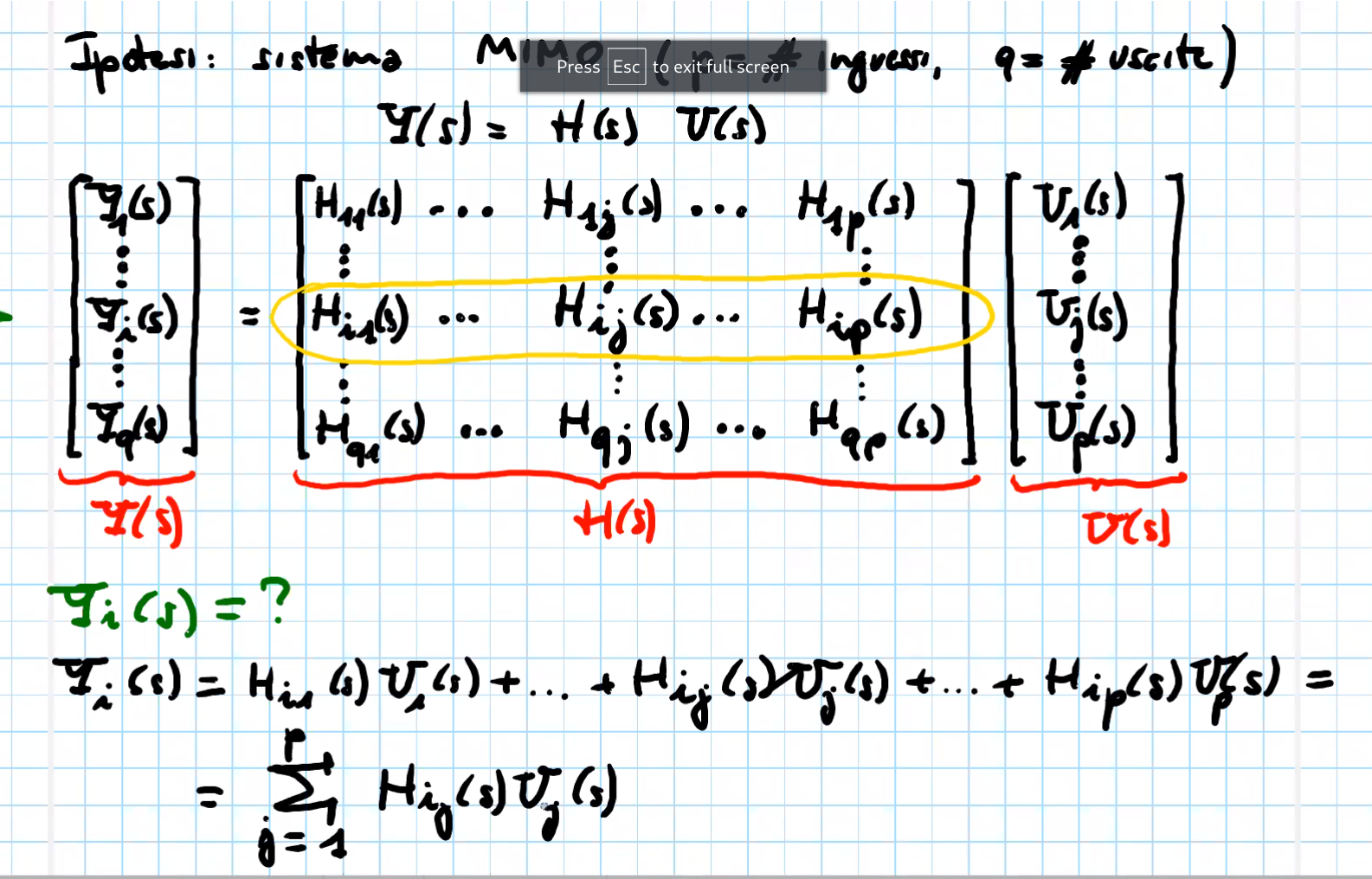
Dunque ogni elemento della matrice di trasferimento è un peso, il peso con cui un certo ingresso influenza una certa uscita.
Dalla sommatoria si vede come una funzione di trasferimento possa essere il rapporto tra l’uscita (una particolare uscita) e un particolare ingresso solo a patto che tutti gli altri ingressi siano spenti (⇒ nei sistemi dinamici LTI TC vale quindi il principio di sovrapposizione).

Rappresentazioni della matrice di trasferimento

Forma polinomiale

La funzione di trasferimento è la matrice $H(s)$ nel sistema SISO, ovvero con un solo ingresso e una sola uscita. La funzione di trasferimento è quindi una funzione razionale fratta e si può scrivere come rapporto tra un polinomio numeratore $N_H(s)$ e un polinomio denominatore $D_H(s)$ uguale al determinante della matrice $(s{I}_n-A)$.
$H(s)=\frac{N_H(s)}{D_H(s)}=\frac{b_m{s}^m+b_{m-1}{s}^{m-1}+\text{...}+b_{1}s+b_0}{a_n{s}^n+a_{n-1}{s}^{n-1}+\text{...}+a_{1}s+a_0},m\le n$
Il fatto che il grado del numeratore non possa essere maggiore del grado del denominatore deriva dalla forma stessa di $H(s)$ come l’abbiamo definita sopra.
A seconda del grado dei polinomi, inoltre, si distinguono:

• funzione di trasferimento strettamente propria se $m<n$ ⇒ in tal caso $b_m=D=0$ ⇒ il sistema è proprio ovvero non c’è una ripercussione istantanea dell’ingresso sull’uscita ma l’uscita dipende solo dalle variabili di stato
• funzione di trasferimento non strettamente propria o più precisamente bipropria se $m=n$; in tal caso il sistema è improprio e si ha $b_m=D\ne 0$.

Forma zeri e poli

In questa forma si vanno ad evidenziare le radici di numeratore (zeri) e denominatore (poli).
$H(s)=K_{\infty }\frac{(s-z_1)(s-z_2)\text{...}(s-z_m)}{(s-p_1)(s-p_2)\text{...}(s-p_n)}$
Il termine $K_{\infty }$ è un guadagno, detto guadagno infinito e si calcola come ${\lim }_{s\to \infty }{s}^{n-m}H(s)$, dove $s^{n-m}$ esiste per far uscire sto limite finito anche nel caso in cui ci siano più zeri che poli.

Forma zeri e poli generalizzata a polinomi aventi radici complesse

Consideriamo il polinomio $p=s^2+a_{1}s+a_0$. Esso ha due radici complesse coniugate che scriviamo come ${\sigma }_0+j{\omega }_0$ e ${\sigma }_0-j{\omega }_0$. (qui si considera ${\sigma }_0$ negativo).
Una scrittura del tipo $p=(s-{\sigma }_0-j{\omega }_0)(s+{\sigma }_0+j{\omega }_0)$ sarebbe quindi corretta, ma sconveniente perchè compare l’unità immaginaria.
Definendo invece pulsazione naturale ${\omega }_n$ e smorzamento $\zeta$ della coppia di radici, dove la pulsazione naturale è la distanza tra lo $0$ e la radice nel piano complesso $\sqrt{{\sigma }_0^2+{\omega }_0^2}$ e lo smorzamento è il seno dell’angolo $\theta$ compreso tra l’asse immaginario e la retta congiungente lo $0$ con la radice. L’angolo è da prendere negativo, se lo vedi andando in senso antiorario come facciamo noi.

Per cui esistono le formule:

• ${\sigma }_0=-\zeta {\omega }_n$
• ${\omega }_0={\omega }_n\sqrt{1-{\zeta }^2}$
• ${\omega }_n=\sqrt{{\sigma }_0^2+{\omega }_0^2}$
• $\zeta =-{\omega }_0\sqrt{{\sigma }_0^2+{\omega }_0^2}$
  In particolare, ${\omega }_n>0$, inoltre $\left|\zeta \right|<1$ per una coppia di radici complesse coniugate. In entrambi i casi non stiamo considerando coppie di radici che si concentrano nell’origine perchè è inutile.
  In definitiva, tutto questo ci permette di scrivere $s^2+a_{1}s+a_2=s^2+2\zeta {\omega }_{n}s+{\omega }_n^2$ e successivamente riscrivere la funzione nella rappresentazione zeri e poli in forma generalizzata per polinomi che presentino sia radici reali sia radici complesse coniugate:
  $H(s)=K_{\infty }\frac{{\prod }_{i=1}^{m_r}(s-z_i){\prod }_{i=1}^{m_c}(s^2+2{\zeta }_{z,i}{\omega }_{nz,i}s+{\omega }_{nz,i}^2)}{{\prod }_{i=1}^{m_r}(s-z_i){\prod }_{i=1}^{m_c}(s^2+2{\zeta }_{p,i}{\omega }_{np,i}s+{\omega }_{np,i}^2)}$
  con, in particolare:
• ${\prod }_{i=1}^{m_r}(s-z_i)$ = prodotto dei fattori che si annullano per via di radici reali
• ${\prod }_{i=1}^{m_c}(s^2+2{\zeta }_{z,i}{\omega }_{nz,i}s+{\omega }_{nz,i}^2)$ = prodotto dei fattori che si annullano per via di radici complesse coniugate
• stessa cosa al denominatore

Forma fattorizzata di Bode (forma fattorizzata in costanti di tempo)

la vediamo quando vediamo le risposte