TAR09.Modellistica di sistemi dinamici TD e trasformata Zeta

Non avremo mai esercizi sulla modellistica di sistemi dinamici a tempo discreto, perchè richiedono linguaggio naturale nel testo.

Sistemi dinamici TD

I sistemi dinamici a tempo discreto sono sistemi in cui le grandezze variabili sono funzioni di una variabile temporale indipendente intera, $k$.
Sono descritti da equazioni di questo tipo:
$x_i(k+1)=f_i(k,x(k),u(k))$
$y_i(k)=g_l(k,x(k),u(k))$
Le equazioni di stato, infatti, sono equazioni alle differenze (invece nel caso del tempo continuo avevamo equazioni differenziali).

Sistemi dinamici a classi di età

Sono introdotti per descrivere l’evoluzione temporale di determinate “classi di popolazione” in periodi di tempo fissati.
(Esempio: parco macchine di noleggio auto, popolazione studentesca, sani e malati).
Ogni variabile di stato $x_i$ rappresenta il numero di elementi che appartengono alla $i$-esima classe (che hanno la proprietà $i$).
I tassi di sopravvivenza e mortalità (che sono l’uno il complementare dell’altro e vanno da $0$ a $1$) mi danno informazioni sull’evoluzione temporale.

Esempio: parco macchine

$x_i(k)$ rappresenta il numero di macchine del parco nell’anno $k$ aventi età $i$ (ovvero aventi età compresa tra $i-1$ e $i$ anni)
$i-1\le \text{etaˋ}(x_i(k))<i$
$u(k)$ rappresenta il numero di macchine nuove che vengono inserite nel parco macchine nell’anno $k$. Non vengono acquistate auto usate.

Supponiamo di non voler avere auto più vecchie di $3$ anni.
Supponiamo che il tasso di mortalità ${\gamma }_i$ sia costante nel tempo.

Classi di età:

• macchine che hanno meno di 1 anno (nuove)
  • $i=1⟹0\le \text{etaˋ}<1$
• macchine che hanno 1 anno
  • $i=1⟹1\le \text{etaˋ}<2$
• macchine che hanno 2 anni
  • $i=2⟹2\le \text{etaˋ}<3$

Equazioni di stato sono allora equazioni alle differenze, quindi c’è il $k+1$, e poi sono facili da scrivere perchè le auto che hanno meno di un anno sono solo e soltanto le auto nuove prese dall’ingresso, invece le auto che hanno $1$ anno sono le auto sopravvissute che l’anno prima avevano meno di un anno, infine le auto che hanno $2$ anni sempre nell’anno $k$ sono quelle sopravvissute che l’anno prima avevano $1$ anno:

$x_1(k+1)=u(k)$
$x_2(k+1)=(1-{\gamma }_1)x_1(k)$
$x_3(k+1)=(1-{\gamma }_2)x_2(k)$
Magari le uscite sono il numero totale di auto nell’anno $k$ ($y_1(k)$) e il costo totale per l’assicurazione di tutte le auto nell’anno $k$ ($y_2(k)$).
$y_1(k)$ è solo la somma di tutte le auto nell’anno $k$, quindi la somma di tutte le variabili di stato:
$y_1(k)=x_1(k)+x_2(k)+x_3(k)$
L’assicurazione costa diversamente rispetto all’età dell’auto:
$y_2(k)=c_1{x}_1(k)+c_2{x}_2(k)+c_3{x}_3(k)$

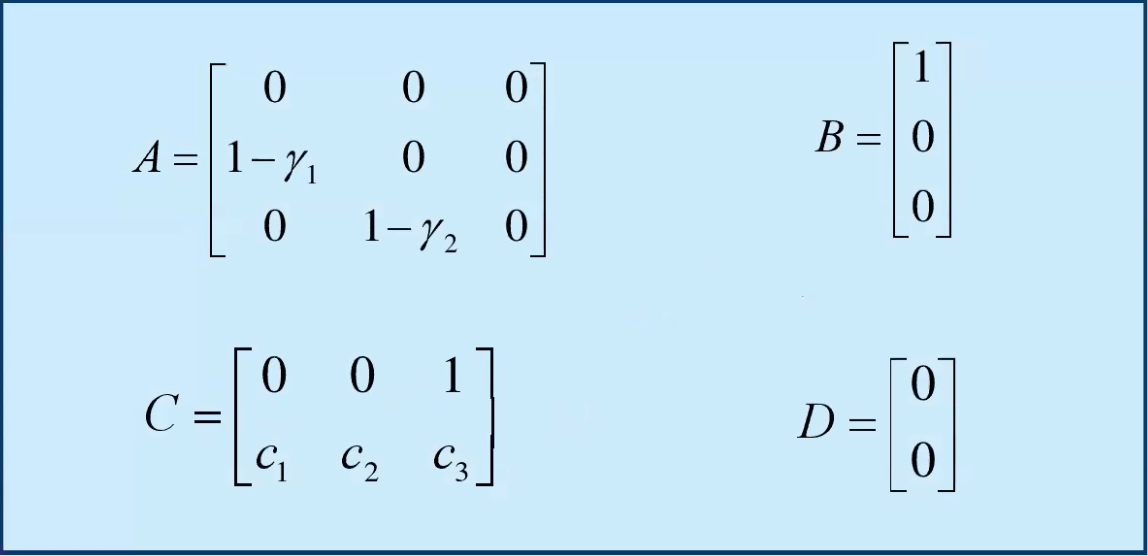
Allora posso rappresentare il sistema come nel caso del tempo continuo, cioè tramite le quattro matrici:

Esempio: popolazione studentesca

Classe $i$-esima: lo studente è formalmente dell’$i$-esimo anno di studio.
Si presuppone nessuno possa inserirsi da altre facoltà negli anni successivi al primo. $u(k)$ sono i nuovi iscritti.
Il tasso di mortalità è pari alla percentuale di bocciati ogni anno e si suppone che ${\gamma }_i$ sia costante nel tempo.
Gli studenti formalmente al primo anno sono la somma dei nuovi studenti appena immatricolati e degli studenti che sono stati bocciati l’anno precedente. Gli studenti che formalmente si trovano ad un anno successivo al primo sono gli studenti “sopravvissuti” all’anno precedente più quelli bocciati dall’anno successivo.
$x_1(k+1)={\gamma }_1{x}_1(k)+u(k)$
$x_2(k+1)=(1-{\gamma }_1)x_2(k)+{\gamma }_2{x}_2(k)$
$x_3(k+1)=(1-{\gamma }_2)x_2(k)+{\gamma }_3{x}_3(k)$
Uscita del sistema: numero di studenti che si diplomano al termini dei tre anni di studio. Cioè, i sopravvissuti al terzo anno:
$y(k)={\gamma }_{3}x(k)$
Le matrici quindi sono:

Sistemi dinamici a dati campionati

Un sistema dinamico a dati campionati tecnicamente è un sistema a TD, con quindi entrata discreta e uscita discreta.
In realtà è costituito da un sistema a tempo continuo, con entrata e uscita continue, che però sono ricavate da convertitori D/A (detto filtro di tenuta) e A/D (detto campionatore).

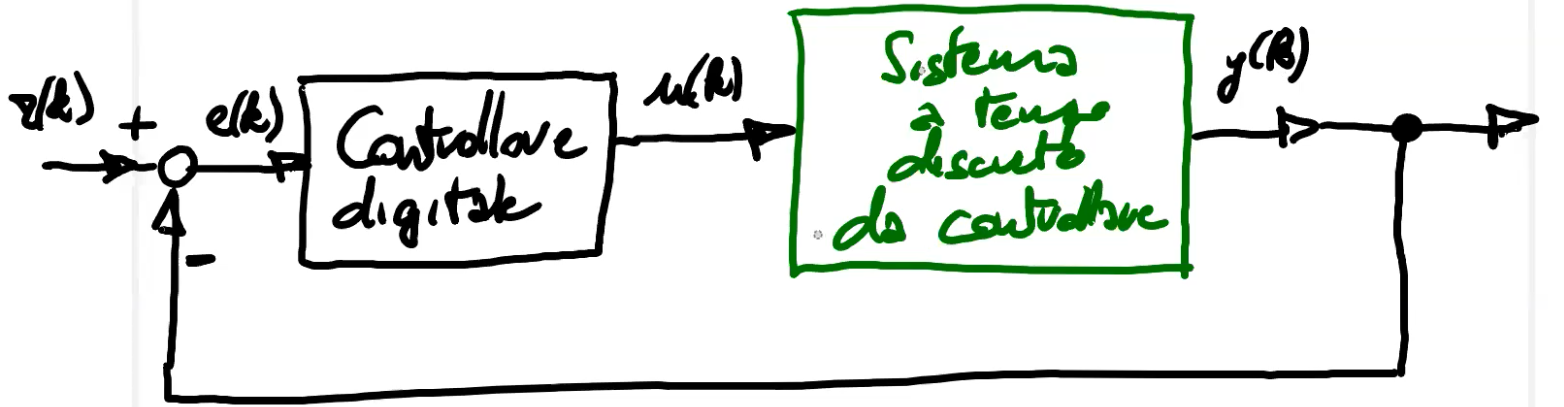
Sistema in cui si usa? ABS.

Discretizzazione

La discretizzazione di un sistema continuo corrisponde a studiare l’evoluzione degli stati, che sono variabili continue, ma solo agli istanti di campionamento. Quindi si parte dalle matrici $A,B,C,D$ e si arriva alle 4 matrici del sistema TD $A_d,B_d,C_d,D_d$ associato al sistema TC secondo la frequenza del campionatore.
Ci sono formule che permettono di fare questo massaggio (bisogna usare la formula di Lagrange con specifici istanti):

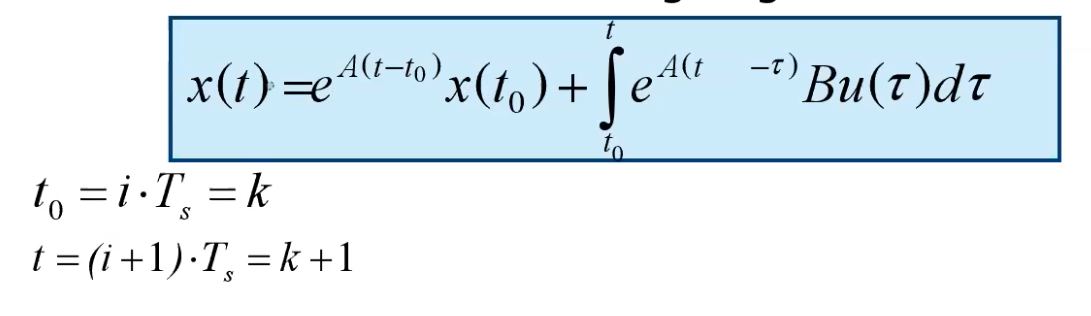
Trasformata Zeta

La trasformata Zeta (unilatera, parte da $0$) della sequenza discreta di valori reali $f(k):\mathbb{N}\to \mathbb{R}$ è la funzione di variabile complessa $z$ definita (quando esiste) da:
$F(z)=\mathcal{Z}\{f(k)\}={\sum }_{k=0}^{\infty }f(k)z^{-k},z\in \mathbb{C}$

Proprietà

• Linearità
• Ritardo nel tempo di $h$ passi
  • $\mathcal{Z}\{f(k-h)\}=z^{-h}F(z)$
• Anticipo nel tempo di $h$ passi
  • $\mathcal{Z}\{f(k+h)\}=z^h(F(z)-{\sum }_{k=0}^{h-1}{z}^{-k}f(k))$
• Prodotto di convoluzione
  • $\mathcal{Z}\{f_1(k)\star f_2(k)\}=F_1(z)\cdot F_2(z)$

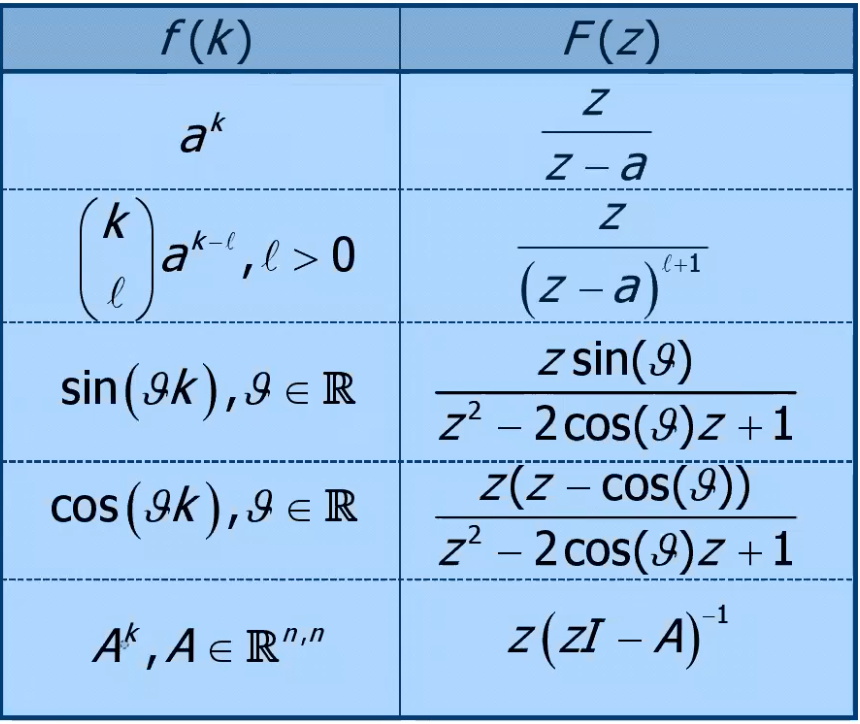
Trasformate notevoli

(la Delta è quella di Kronecher, quindi arriva ad 1 non ad infinito)

Accorgimenti nella scomposizione in fratti semplici

Come risolvo sta cosa? Non ho delle $z$ al numeratore.
Allora non mi conviene mai proseguire così:
per non avere problemi, mi conviene partire con una funzione di trasferimento pre-divisa per $z$, successivamente fare la anti-trasformazione e solo dopo moltiplicare per $z$:

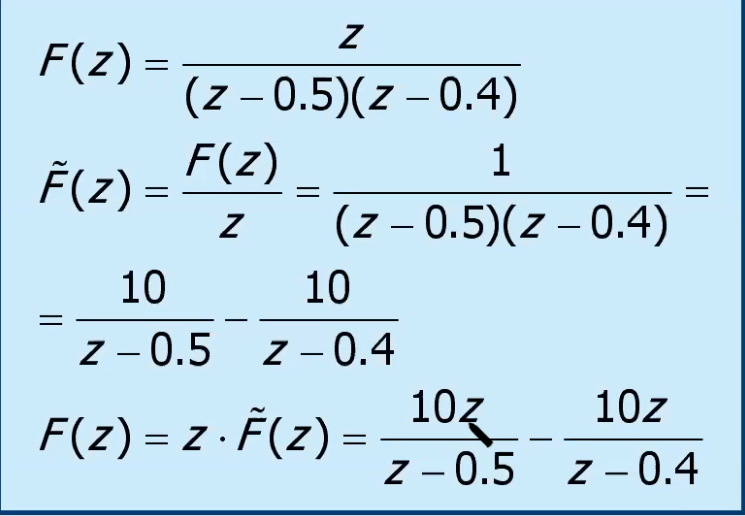
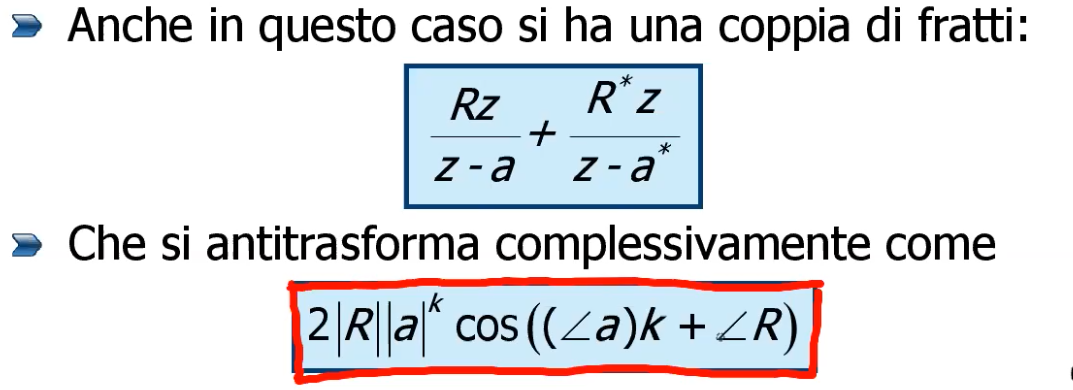
Nel caso delle coppie di radici complesse coniugate: