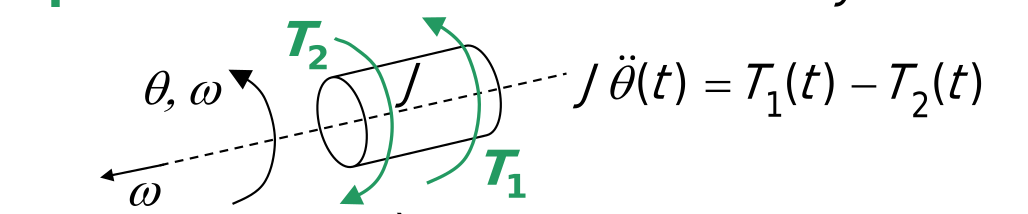TAR03.Modellistica di sistemi meccanici

Sistemi in traslazione

Elementi fondamentali

• Molla ideale
  • $K[p_{+}(t)-p_{-}(t)]$
  • $p$ sono le posizioni relative delle estremità della molla
• Smorzatore ideale
  • $\beta [v_{+}(t)-v_{-}(t)]=\beta [{\dot{p}}_{+}-{\dot{p}}_{-}(t)]$
  • $v$ sono le derivate delle posizioni relative delle estremità dello smorzatore, ovvero le loro velocità relative

Equazioni del moto per sistemi in traslazione

• Si introducono assi di riferimento concordi fra loro per indicare le posizioni di ogni corpo in traslazione;
• Per ogni massa $M_i$ con posizione $p_i$ e velocità $v_i={\dot{p}}_i$, vale la seconda legge di Newton scritta come:
  • $M_i{a}_i=M_i{\ddot{p}}_i(t)=\sum F_k^{\text{est}}(t)-\sum F_k^{\text{int}}(t)$
• con le forza interne $F$ che tengono conto dell’interazione tra l’elemento $M_i$ considerato e gli altri corpi $M_j$ tramite:
  • Molle ideali
    • $K_{ij}[p_i(t)-p_j(t)]$
  • Smorzatori ideali
    • ${\beta }_{ij}[{\dot{p}}_i(t)-{\dot{p}}_j(t)]$
• Quindi sempre “la $p$ (o $v$) del corpo che sto considerando in questo momento $-$ l’altra”.

Rappresentazione in variabili di stato

• Si scrivono le equazioni del moto per ogni corpo puntiforme di massa $M_i$ (eventualmente nulla) in traslazione, avente posizione $p_i$ e velocità $v_i={\dot{p}}_i$
• Si introducono due variabili di stato ($p_i$ e $v_i$) per ogni elemento $M_i$ in traslazione. Si scelgono due variabili perchè le equazioni “costitutive” degli elementi del sistema sono equazioni differenziali del secondo ordine (appare la derivata seconda, l’accelerazione). Questo permette di trasformare le equazioni differenziali del secondo ordine in coppie di equazioni differenziali del I ordine
• Variabili di ingresso sono le forze esterne. Queste forze devono essere maneggiabili dall’utente (es. forza di gravità non è da esplicitare perchè indipendente e costante)
• Si ricavano le equazioni di stato, che sono sempre nella forma di equazioni differenziali ordinarie del primo ordine.
  • sono in una forma tale che le prime due equazioni di stato sono semplicemente ${\dot{x}}_1=x_3$ e ${\dot{x}}_2=x_4$
• Si scrivono le equazioni di uscita (che sono istantanee, come al solito)
  Esercizio su quaderno Slide 38.
  PS: per catturare l’effetto dell’attrito viscoso si può considerare di mettere in parallelo ad eventuali smorzatori / molle già presenti un ulteriore smorzatore e / o considerare uno smorzatore equivalente avente come $\beta$ la somma dei vari $\beta$ degli smorzatori.
  Nel caso si volessero considerare effetti come quello dell’attrito radente o dello smorzamento coulombiano, si può aggiungere uno smorzatore con un $\beta$ opportuno (non costante).
  Esercizio su quaderno su levitatore magnetico
  Esercizio su quaderno con punto materiale a massa nulla (slide 94) - si vede che non va bene prendere ${\dot{p}}_A$ come variabile di stato, perchè si scopre non essere linearmente indipendente dalle altre variabili di stato (in particolare, ${\dot{p}}_A$ dipende da $\dot{p}$ e $p_A$). In tal caso la si butta e si considera una variabile di stato in meno.
  I punti materiali sono l’equivalente delle reti elettriche degeneri nal caso di sistemi elettrici.
  Inoltre, si vede una variabile di uscita che non serve perchè nessuno è interessato (quindi si può buttare via sia l’uscita sia la variabile di stato, dato che da essa dipendeva solo quella stessa uscita).
  Morale della favola… non considerare proprio le leggi del moto dei punti materiali se nessuno è interessato alle loro variabili in uscita. Comunque non considerare come variabili di stato le accelerazioni dei punti materiali, perchè non saranno ricavabili dall’equazione del moto ($M_A\ddot{p_A}=0\forall \ddot{p_A}\text{ se }{M}_A=0$)

Sistemi in rotazione

Si consideri un sistema di riferimento per cui una rotazione in senso antiorario individua un vettore coppia $\vec{T}$ positivo.

• Utile disegnare in 2D, considerando una sezione dello spazio 3D che contenga l’asse di rotazione.

Elementi fondamentali

• Corpo puntiforme in rotazione di inerzia $J$ e coppia di inerzia $J\ddot{\theta }(t)$, con $\theta (t)=$ velocità angolare del corpo ($T=$ torque, coppia). La coppia si indica come vettori rotanti o con un vettore $\vec{T}$ che esce seguendo la regola della mano destra rispetto ai vettori rotanti.
  • $J\ddot{\theta }(t)=J\frac{d^2\theta (t)}{d{t}^2}=T(t)$
  • 
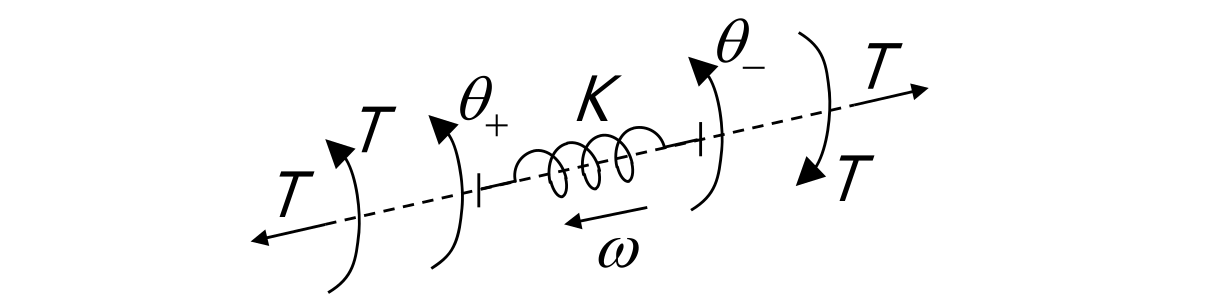
• Molla ideale
  Caratterizzata dalla coppia elastica
  $T(t)=K[{\theta }_{+}(t)-{\theta }_{-}(t)]$
  
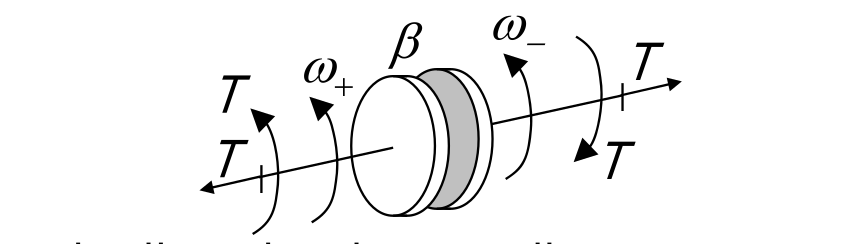
• Smorzatore ideale
  Caratterizzato dalla coppia di attrito
  $T(t)=\beta [{\omega }_{+}(t)-{\omega }_{-}(t)]=\beta [{\dot{\theta }}_{+}(t)-{\dot{\theta }}_{-}(t)]$
  

Equazioni del moto

$J_i{\ddot{\theta }}_i(t)={\Sigma }_k{T}_k^{\text{est}}(t)-{\Sigma }_l^{l\ne i}{T}_{il}^{\text{int}}(t)$
Le coppie interne dipendono da molle e smorzatori.

Rappresentazione in variabili di stato

• Si scrivono le equazioni del moto (per non sbagliare i segni: nella parentesi quadra va “la variabile del corpo considerato - quella dell’altro, sempre”).
• Introduco come variabili di stato ${\theta }_i$ e ${\dot{\theta }}_i$, per trasformare le equazioni del moto, differenziali del II ordine, in equazioni differenziali del primo ordine (se un corpo ha momento di inerzia nullo, non considerare la sua velocità angolare come variabile di stato).
  • ${\dot{x}}_1=x_3$, ${\dot{x}}_2=x_4$ anche qui
• Introduco variabili di ingresso (forze esterne) e variabili di uscita.
• Si fa la solita roba algebrica.
  • In particolare, si arriva che dovrai dividere per la massa ambo i membri
    Esempio su quadernetto.