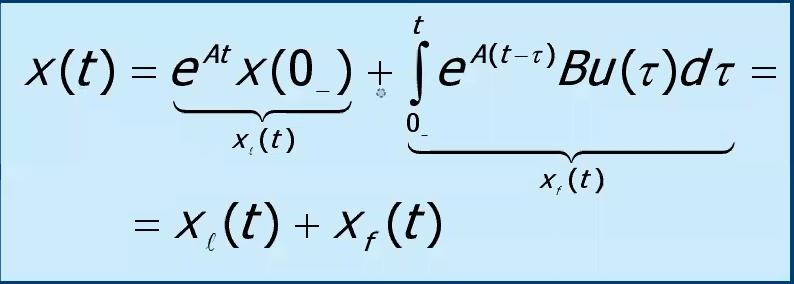TAR10.Analisi nel dominio del tempo e della trasformata Zeta di sistemi dinamici LTI TD

Soluzione nel dominio del tempo (e confronto con TC)

RECAP: Nel caso del sistema a TC, la soluzione nel dominio del tempo era effettivamente troppo complessa per dei giovani ingegneri sbarbatelli che col cazzo che conoscono la matematica, perchè infatti nel tempo l’unico modo di risolvere era tramite la formula di Lagrange, con la matrice esponenziale e un prodotto di convoluzione:
Allora ci eravamo inventati di usare la trasformata di Laplace, per spostarci nel dominio della frequenza, risolvere in quel dominio (più semplice) e successivamente tornare nel dominio del tempo con un’antitrasformazione del risultato.In particolare, nei sistemi TC l’equazione di stato era del tipo differenziale, come
$\dot{x}(t)=Ax(t)+Bu(t)$
Di conseguenza, prima dicevamo che
$X(s)=(sI-A{)}^{-1}x(0^{-})+(sI-A{)}^{-1}BU(s)$ e poi antitrasformata, e via.

Nel dominio del tempo discreto la soluzione è invece facile da scrivere, infatti abbiamo un’equazione alle differenze e non un’equazione differenziale come equazione di stato.
$x(k+1)=Ax(k)+Bu(k)$
Questo ci permette di calcolare il movimento di $x(k)$ semplicemente con un processo iterativo (posto di conoscere le condizioni iniziali, così come era nel TC) invece di dover fare la formula di Lagrange:
$x(1)=Ax(0)+Bu(0)$
$x(2)=Ax(1)+Bu(1)=A^{2}x(0)+ABu(0)+Bu(1)$
$...$
$x(k)=A^{k}x(0)+{\sum }_{i=0}^{k-1}{A}^{k-i-1}Bu(i)$
Anche qui possiamo distinguere i due addendi come un movimento libero e un movimento forzato.
$x(k)=A^{k}x(0)+{\sum }_{i=0}^{k-1}{A}^{k-i-1}Bu(i)=x_l(k)+x_f(k)$

In verità non è che non stiamo facendo la formula di Lagrange, ma nel caso di tempo discreto essa si specializza in questo modo, infatti se vedi bene il secondo termine sembra una convoluzione in trasformata zeta, vabbè lo so che non ti interessa.

Dominio della trasformata Zeta

Passare nel dominio della zeta è comunque un metodo più veloce rispetto a fare quel metodo iterativo lì, che poi tra l’altro diventa probabilmente unfeasible nel caso in cui stai cercando di calcolare qualcosa come $x(452)$.
Come al solito, passiamo nel dominio della $z$, svolgiamo i conti, e torniamo indietro, nel dominio della $k$.

In particolare vanno trasformate le equazioni di stato e uscita:

• L’equazione di stato nel TD è un’equazione alle differenze, quindi compare $k+1$, che altro non è se non un anticipo nel tempo discreto di $1$ passo $⟹$ ho una formula:
  • $\mathcal{Z}\{f(k+h)\}=z^h(F(z)-{\sum }_{k=0}^{h-1}{z}^{-k}f(k))$
    • $h=1⟹\mathcal{Z}\{x(k+1)\}=zX(z)-zx(0)$
      • notare la $z$ che moltiplica la condizione iniziale, che nel dominio di Laplace non c’era
  • $zX(z)-x(0)=AX(z)+BU(z)$
    • $X(z)=z(zI-A{)}^{-1}x(0)+(zI-A{)}^{-1}BU(z)=$
    • $=X_l(z)+X_f(z)$
      • notare che qui c’è una $z$ che moltiplica nell’espressione del movimento libero, cosa che nel dominio di Laplace non c’era
  • poi basta antitrasformare
• Per l’uscita basta sostituire la $X(z)$ trovata prima, ed esce:
  • $Y(z)=zC(zI-A{)}^{-1}x(0)+[C(zI-A{)}^{-1}B+D]U(z)=$
  • $=Y_l(z)+Y_f(z)$
    • La parte $C(zI-A{)}^{-1}B+D$ è considerabile la funzione di trasferimento del sistema.