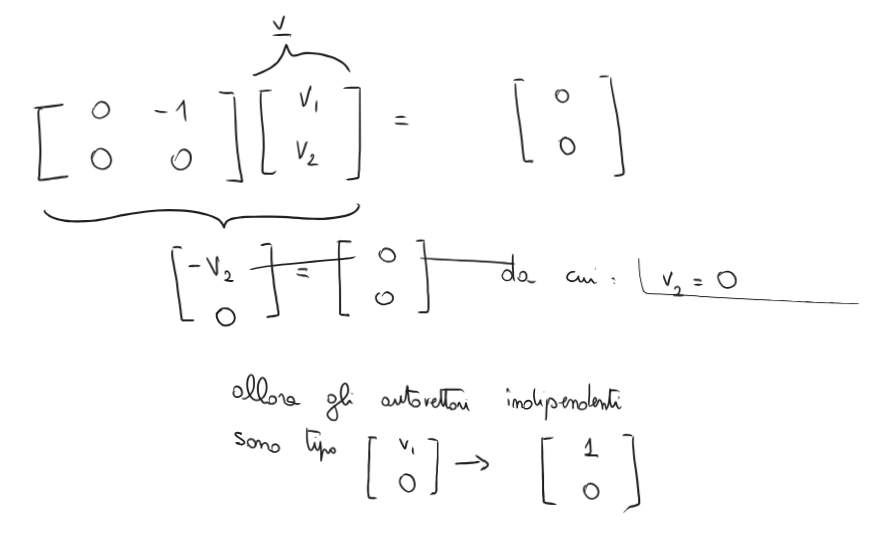TAR08.Analisi modale di sistemi dinamici LTI TC

Confronto con analisi tramite Laplace

L’analisi modale è più semplice di quella tramite Laplace e non ha come scopo la determinazione in ogni istante dell’evoluzione dello stato $x(t)$, ma invece si propone di fornire informazioni più qualitative ad una frazione dello sforzo.
Ma solo sul movimento libero del sistema.

Modi naturali di un sistema dinamico

Consideriamo solo l’evoluzione libera dello stato, quindi se $\dot{x}(t)=Ax+Bu$
consideriamo solo la parte $\dot{x}(t)=Ax$.
$x(t)=x_l+x_f$ e dalla formula di Lagrange si vede che $x_l(t)=e^{At}x(0^{-})$, quindi mi serve lo stato iniziale noto e mi serve anche la matrice esponenziale.

Matrice esponenziale

La matrice esponenziale $e^{At}$, ponendo che sia $A$ una matrice diagonale e con $n$ autovalori reali e distinti, non è altro che una matrice diagonale a sua volta, con sulla diagonale principale $e^{{\lambda }_{i}t}$, per ogni autovalore ${\lambda }_i$.

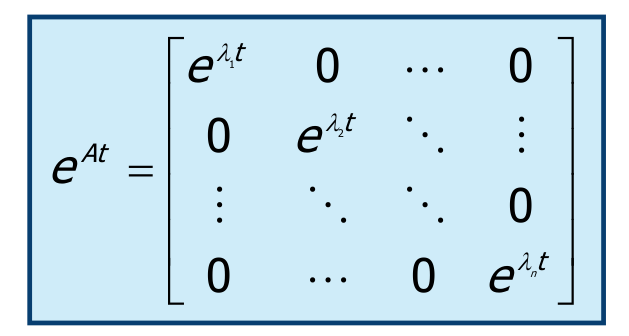
Ogni funzione del tipo $e^{{\lambda }_{i}t}$ è un modo naturale (o modo proprio) del sistema associato all’autovalore ${\lambda }_i$.
In generale, le espressioni analitiche dei modi naturali non sono di forma semplicemente esponenziale e dipendono dal fatto che gli autovalori siano reali o complessi e dalla loro molteplicità.

Analisi modale

Studiare il comportamento dei modi naturali in base alle caratteristiche degli autovalori associati si chiama analisi modale.
In particolare si studia il comportamento dei modi naturali per $t\to \infty$.
Ci da informazioni sul movimento libero dello stato di un sistema dinamico senza dover risolvere tutto e calcolarne l’espressione anaiitica.

Un modo naturale $m(t)$ è:

• convergente se ${\lim }_{t\to \infty }|m(t)|=0$
• limitato se ${\lim }_{t\to \infty }|m(t)|\le M<\infty$
• divergente se ${\lim }_{t\to \infty }|m(t)|=\infty$

Per trovare i modi naturali, bisogna conoscere gli autovalori della matrice $A$. Questo è immediato solo se $A$ è già diagonale / diagonale a blocchi / triangolare / triangolare a blocchi, perchè tra l’altro ha tutti gli autovalori in bella vista sulla diagonale principale, oppure sono facilmente calcolabili.
Negli altri casi, gli autovalori si trovano risolvendo l’equazione caratteristica $\det (A-\lambda I)=0$, il che può essere più o meno semplice in base alle caratteristiche della matrice in esame.

Matrice in forma di Jordan associata

Per calcolare gli autovalori di una matrice nel caso in cui questa non sia in una delle forme per cui è semplice farlo, è necessario prima operare un’operazione di cambio di base tramite un prodotto di similarità (a panino) che mi faccia arrivare ad una matrice più semplice, che però abbia gli stessi autovalori.
$x_l=e^{At}x(0^{-})=T{e}^{\tilde{A}t}{T}^{-1}x(0^{-})$
dove $\tilde{A}$ è una matrice in forma di Jordan, ovvero diagonale a blocchi dove ogni blocco è associato ad uno specifico autovalore.

Forma dei blocchi

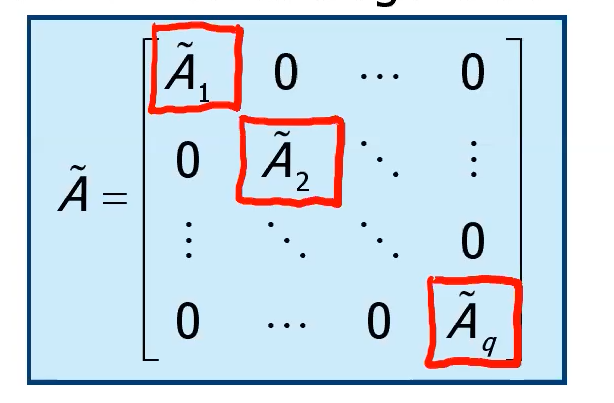
I blocchi della matrice $e^{\tilde{A}t}$ hanno forme note, in particolare:

Blocchi corrispondenti ad autovalori reali a molteplicità unitaria

I blocchi corrispondenti agli autovalori di $A$ che sono reali e distinti e hanno molteplicità unitaria sono in realtà da un solo elemento, $e^{{\lambda }_{i}t}$

I modi naturali che ne escono sono quindi del tipo $e^{{\lambda }_{i}t}$

Se $A$ ha solo autovalori di questo tipo, $e^{\tilde{A}t}$ esce così:

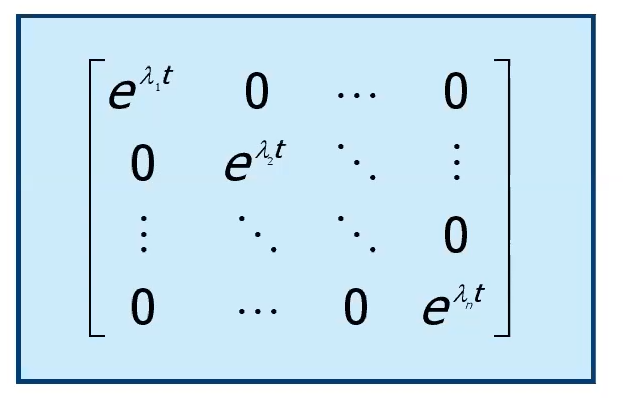
Un modo naturale associato ad un autovalore reale di molteplicità unitaria è esattamente $=e^{{\lambda }_{i}t}$, quindi è ulteriormente definibile come:

• esponenzialmente convergente: $\Re (\lambda )<0$ (es. $e^{-2t}$)
• limitato (costante): $\Re (\lambda )=0$ (es. $e^{0t}=ϵ(t)$)
• esponenzialmente divergente: $\Re (\lambda )>0$ (es. $e^t$)

Blocchi corrispondenti a coppie di autovalori complessi coniugati a molteplicità unitaria

I blocchi corrispondenti alle coppie di autovalori complessi coniugati di $A$ con molteplicità unitaria, scritti come $\lambda =\sigma \pm j\omega$ sono invece del tipo: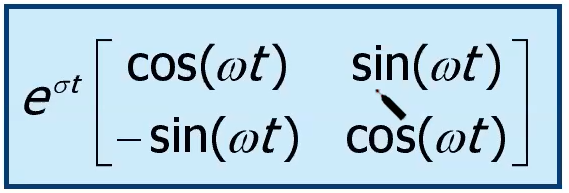
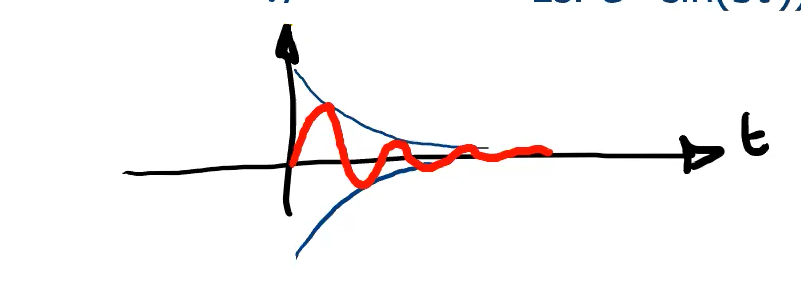
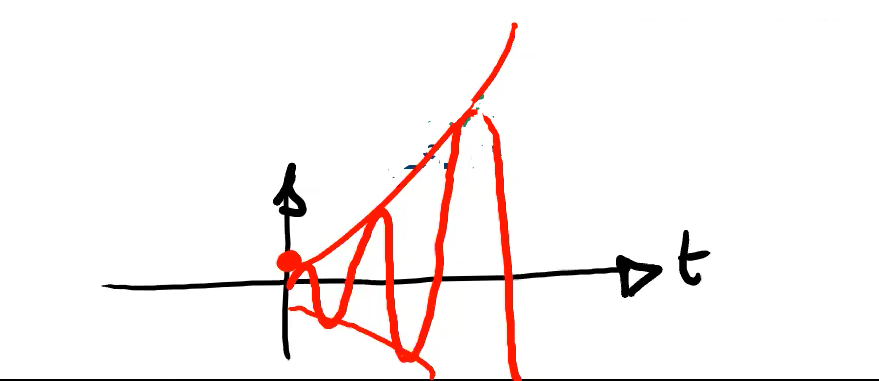
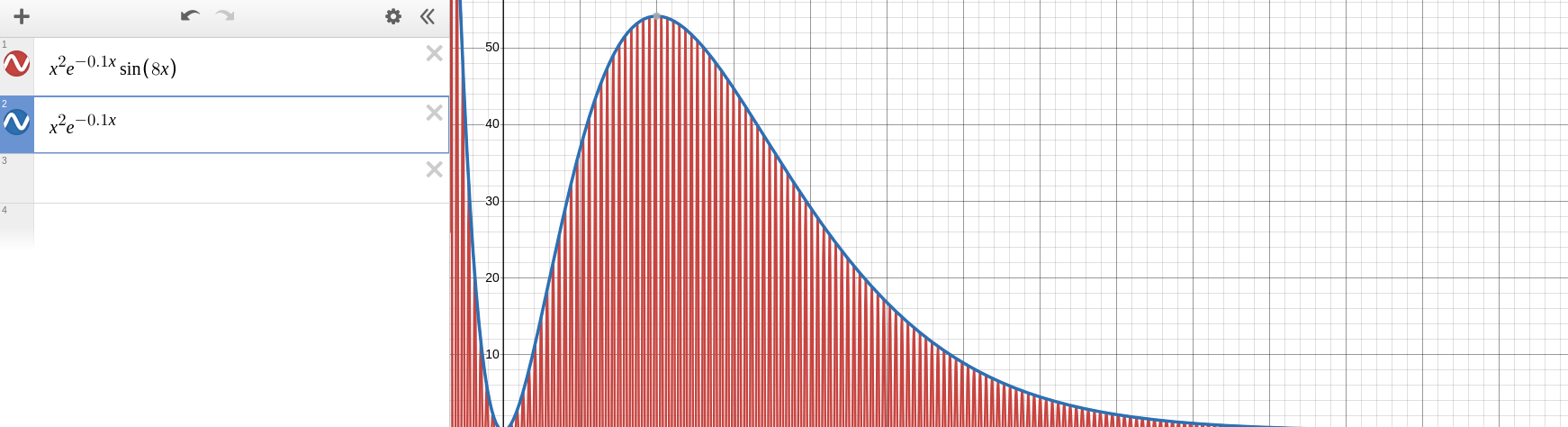
I modi naturali che ne escono sono del tipo $e^{\sigma t}\cos (\omega t)$, $e^{\sigma t}\sin (\omega t)$, quindi sono oscillanti. $e^{\sigma t}$ è detto inviluppo.

Essi possono essere classificati come

• esponenzialmente convergente: $\sigma <0$ (es. $e^{-t}\cos (t$))
  • 
• limitato (oscillante): $\sigma =0,\omega \ne 0$ (es. $\sin (5t$))
• esponenzialmente divergente: $\sigma >0$ (es. $e^{2t}\sin (t$))
  • 

Blocchi corrispondenti ad autovalori reali a molteplicità multipla

I blocchi associati ad autovalori reali di molteplicità algebrica $\mu >1$ (che annullano il polinomio caratteristico più volte) sono a loro volta matrici diagonali a blocchi, contententi a loro volta (di nuovo) delle sottomatrici triangolari del tipo:
I modi naturali associati a questi autovalori sono, in numero, ${\mu }^{\prime }\le \mu$ (${\mu }^{\prime }=$ molteplicità geometrica dell’autovalore).

Info

Calcolo di ${\mu }^{\prime }$
La molteplicità geometrica di un autovalore di una matrice $A$ è il numero di autovettori linearmente indipendenti associati all’autovalore.
Se vuoi proprio farlo, devi fare il calcolo “quasi esplicito” degli autovalori; cioè imposti
$(\lambda I_n-A)\vec{v}=[00{]}^T$
e vedi quanti vincoli ti si vengono a creare.
${\mu }^{\prime }=\mu -d+1\ge \mu$
Esempio:

Infatti $v_2=0$ è un vincolo e quindi $d=1$.

Il discorso è che tanto non ti serve davvero calcolare sta cosa, in quanto sia $t^5{e}^{\sigma }t$ che $t^{5456}{e}^{\sigma }t$ seguono l’andamento dell’esponenziale, che come direbbe Simone, è più forte.

I modi naturali che ne vengono fuori sono del tipo $t^{{\mu }^{\prime }-1}{e}^{\lambda t},t^{{\mu }^{\prime }-2}{e}^{\lambda t}...e^{\lambda t}$ e possono essere classificati come

• esponenzialmente convergenti: $\lambda <0$ (es. $t^5{e}^{-t}$)
• polinomialmente divergenti: $\lambda =0$ (es. $t^2$)
• esponenzialmente divergenti: $\lambda >0$ (es. $t^5{e}^{2t}$)

Blocchi corrispondenti a coppie di autovalori complessi coniugati a molteplicità multipla

I blocchi associati a coppie di autovalori complessi coniugati di molteplicità algebrica $\mu >1$ hanno forma analoga al caso reale.

Danno origine a ${\mu }^{\prime }\le \mu$ modi naturali, che hanno forma $t^{{\mu }^{\prime }-1}{e}^{\sigma t}\cos (\omega t),...e^{\sigma t}\cos \omega t$ e $t^{{\mu }^{\prime }-1}{e}^{\sigma t}\sin (\omega t),...e^{\sigma t}\sin (\omega t)$.
Sono comunque oscillanti.

Si possono classificare come:

• esponenzialmente convergenti: $\sigma <0$
• polinonialmente divergenti: $\sigma =0$
• esponenzialmente divergenti: $\sigma >0$

Info

In questo caso l’inviluppo è la moltiplicazione della parte polinomiale con la parte esponenziale del modo.

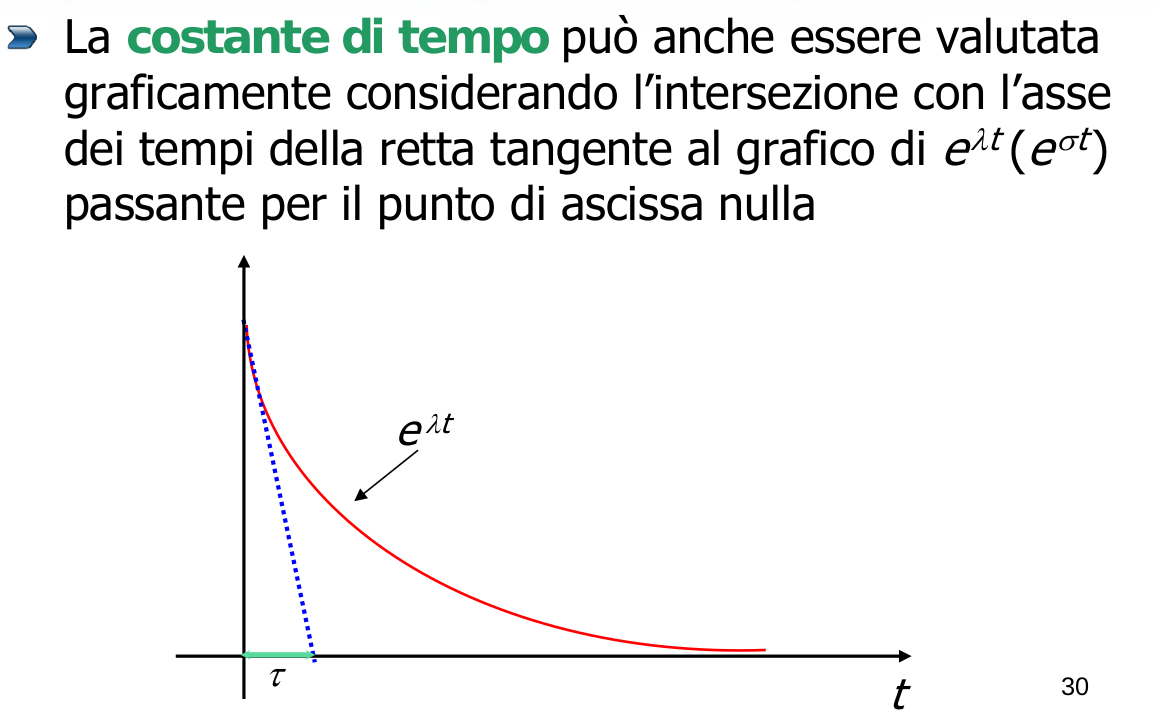
Costanti di tempo dei modi naturali

Per ogni autovalore con parte reale negativa, si definisce la costante di tempo ad esso associata come
$\tau =\left|\frac{1}{\Re (\lambda )}\right|$
Questa costante di tempo è la costante di tempo del modo naturale associato (convergente), cioè rappresenta una misura della rapidità con la quale $e^{{\lambda }_{i}t}$ scende a $0$.

Esempio: il modo $e^{-2t}$ ha costante di tempo $0.5$ s, quindi converge a zero più rapidamente di $e^{-t}$, che ha costante di tempo $1$ s.