TAR22a.Risposte di sistemi del I ordine

Introduzione

L’analisi della risposta di un sistema dinamico ad un dato ingresso standard (il gradino e l’impulso) è di fondamentale importanza per quei casi in cui si vuole arrivare alle caratteristiche del sistema partendo da dati empirici (do al sistema, che considero una “scatola nera”, in pasto una serie di ingressi noti, vedo le uscite, non conosco come è fatto dentro).
È possibile infatti, a partire da dati empirici, ricavare parametri caratteristici del sistema, quindi costruire dei modelli semplificati (la funzione di trasferimento di questi modell semplificati magari ha un comportamento che si sovrappone spesso a quello della funzione di trasferimento effettiva implementata dal sistema reale, ma magari non precisamente in ogni punto) del sistema senza conoscere la sua struttura interna.

Parleremo solo dei sistemi LTI (TC), notando che questo tipo di analisi è particolarmente utile nel caso di sistemi LTI esternamente stabili (funzione di trasferimento con solo poli a parte reale strettamente negativa). In questi casi, infatti, è possibile partendo dai soli dati sperimentali studiare il comportamento del sistema nella transizione da uno stato di equilibrio ad un altro, e in alcuni casi, di determinare esattamente la funzione di trasferimento del sistema, in quanto esce una congruenza tra il modello semplificato che costruisco e quello effettivo.

La funzione di trasferimento del sistema LTI TC è
$H(s)=C(s{I}_n-A{)}^{-1}B+D$
e si può scrivere come una funzione razionale fratta:
$H(s)=\frac{N_H(s)}{D_H(s)}$
Con $N_H$ e $D_H$ polinomi senza radici in comune. Quando $D_H$ è un polinomio di primo grado, la funzione di trasferimento è detta del primo ordine, quando è di secondo grado, del secondo ordine, ecc.
I sistemi, inoltre, sono detti elementari se la loro funzione di trasferimento è strettamente propria (ovvero se $\mathrm{deg}(N_H)<\mathrm{deg}(D_H)$).

Analisi della risposta di sistemi di I grado

Le premesse che il sistema deve rispettare per poter procedere all’analisi secondo quanto segue sono:

• la funzione di trasferimento deve essere strettamente propria
• la funzione di trasferimento deve presentare unicamente poli a parte reale strettamente negativa $⟹$ la funzione non divergerà mai ad infinito $⟺$ (si, doppia implicazione, se e solo se) la funzione il sistema è esternamente stabile nel senso della BIBO-stabilità (ad un Bounded Input corrisponde sempre un Bounded Output)
• il sistema è considerato inizialemente a riposo, ovvero $x(0^{-})=0$ (la risposta libera si annulla e la risposta del sistema è quindi identica alla sola risposta forzata)

in questi casi, considerando gli ingressi specifici di gradino e impulso, ovvero:
$u=\overline{u}ϵ(t)$
$u=\overline{u}\delta (t)$
che nel dominio della trasformata di Laplace diventano:
$U=\overline{u}/s$
$U=\overline{u}$
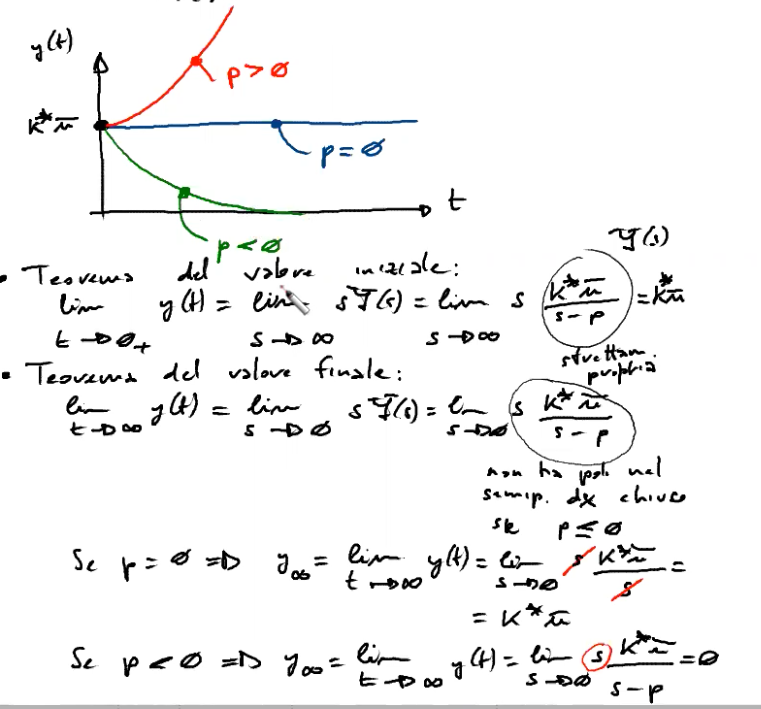
Possiamo dire, conoscendo $y(t)$ e quindi $Y(s)$, che
$Y(s)=H(s)U(s)$
Si ricordino i teoremi:

• del valore iniziale: ${\lim }_{t\to 0^{+}}y(t)={\lim }_{s\to +\infty }sY(s)$, se entrambi i limiti esistono e sono finiti (basta verificare in particolare che la FdT sia strettamente propria)
• del valore finale: ${\lim }_{t\to +\infty }y(t)={\lim }_{s\to 0}sY(s)$, se entrambi i limiti esistono e sono finiti (basta verificare in particolare che $sY(s)$ non abbia poli nel semipiano destro chiuso ($=$ incluso $0$) $⟹$ $sY(s)$ deve avere tutti i poli a parte reale strettamente negativa)

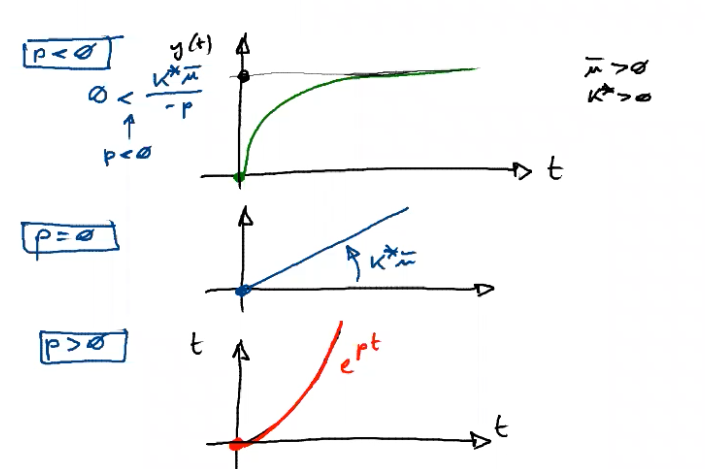
Risposte di sistemi del primo ordine

$\mathrm{deg}(D_H)=1$, quindi $\mathrm{deg}(N_H)=0⟹$ il numeratore è una costante
$H(s)=\frac{K^{\star }}{s-p}$
($p$ è l’unico polo della FdT). In questo caso la FdT scritta in forma polinomiale equivale alla scrittura in forma zeri-poli.

Risposta all’impulso

Se $u(t)=\overline{u}\delta (t)⟹U(s)=\overline{u}$ allora la risposta forzata (che coincide con l’intera risposta) è
$Y(s)=H(s)\overline{u}=\frac{K^{\star }}{s-p}\overline{u}$
Posso tranquillamente anti-trasformare per ottenere
$y(t)=K^{\star }\overline{u}{e}^{pt}ϵ(t)$
ovvero la risposta all’impulso è un esponenziale, divergente se $p>0$, convergente a $0$ se $p<0$, e degenera in una costante per $p=0$.

Il grafico della risposta parte sempre dal punto $(0,K^{\star }\overline{u})$.

I teoremi di valore iniziale e finale, quando sono applicabili, ci confermano il tutto.

Risposta al gradino

Se $u(t)=\overline{u}ϵ(t)⟹U(s)=\overline{u}/s$ allora la risposta forzata (che coincide con l’intera risposta) è
$Y(s)=H(s)\frac{\overline{u}}{s}=\frac{K^{\star }}{s(s-p)}\overline{u}$
Abbiamo quindi due poli, $s=0$ e $s=-p$.
Il caso $p=0$ lo possiamo trattare separatamente, in quanto è più facile: al denominatore non abbiamo più un polo in $s=-p$ ma un polo di molteplicità $2$ in $s=0$. In questo caso l’antitrasformata ha la forma specifica:
$y(t)=K^{\star }\overline{u}tϵ(t)$

• se $p\ne 0$, invece, converrà fare la scomposizione in fratti semplici, e poi antitrasformare per ottenere:
  • $y(t)=\frac{K^{\star }}{-p}\overline{u}[1-e^{pt}]ϵ(t)$
  • 

ovvero la risposta al gradino converge esponenzialmente per $p<0$, diverge linearmente se $p=0$, diverge esponenzialmente per $p>0$.

Ma allora a che servono i teoremi di valore finale e iniziale?
Semplice, in questi casi ho il grafico già fatto dal professore. Nella mia solita vita nessuno mi dice $y(t)=\frac{K^{\star }}{-p}\overline{u}[1-e^{pt}]ϵ(t)$ che andamento ha sul grafico, anche se è immaginabile in questo caso, in altri casi rischio di dover fare studi e controstudi di funzione.
Allora i teoremi di valore finale e iniziale, quando applicabili, mi salvano dal disastro, dandomi un’altra via per arrivare alle uniche informazioni che mi servono: da dove parte, dove finisce.

Una considerazione: dato che nella vita vera è impossibile sottoporre un impulso come ingresso, la risposta al gradino è quella su cui realmente si lavora.

In questo caso il teorema del valore iniziale è applicabile e ci da come risultato $0$.
Il teorema del valore finale è invece applicabile solo nel caso $p<0$ (nessun polo nel semipiano destro chiuso $⟹$ BIBO-stabile) - ci dice allora che il valore finale è $\frac{K^{\star }}{-p}\overline{u}$.

Parametri specifici per risposta al gradino di sistemi del I ordine BIBO-stabili

Nelle risposte di questo tipo di sistemi BIBO-stabili chiamiamo $\frac{K^{\star }}{-p}=K$ e quindi diciamo che il valore finale è $K\overline{u}$. Inoltre chiamiamo $\left|\frac{1}{p}\right|=\tau >0$ costante di tempo del sistema.
Allora si può anche scrivere la $H(s)$ come
$H(s)=\frac{K}{1+\tau s}$
(forma di Bode).

• Nel caso $p<0$ è importante anche il tempo di salita $t_r$ che è il tempo che l’uscita impiega a portarsi dal $10\%$ al $90\%$ del valore finale.
• Il tempo di assestamento ad un certo percentile $t_{a,ϵ\%}$ è il tempo necessario ad arrivare ad una situazione in cui la risposta del sistema non avrà mai variazioni tali da differire dal valore finale (di regime, $y_{\infty }$) più di un certo percentile, ovvero più del $ϵ\%$ del valore finale stesso.
  • Noi useremo il $t_{a,5\%}$.
  • È importante notare che nei sistemi di I ordine il tempo di assestamento al $5\%$ è sempre coincidente con $3\tau$ (dopo $3\tau$ l’uscita è arrivata al $95\%$ del valore finale).
• Invece, è un trivia utile da sapere che dopo $1\tau$ la risposta del sistema arriva sempre intorno al $63\%$ del valore di regime.

Cercheremo di generalizzare questi concetti per i sistemi del secondo ordine, che tecnicamente non hanno una costante di tempo, ma c’è un valore che si può considerare equivalente ad una costante di tempo.

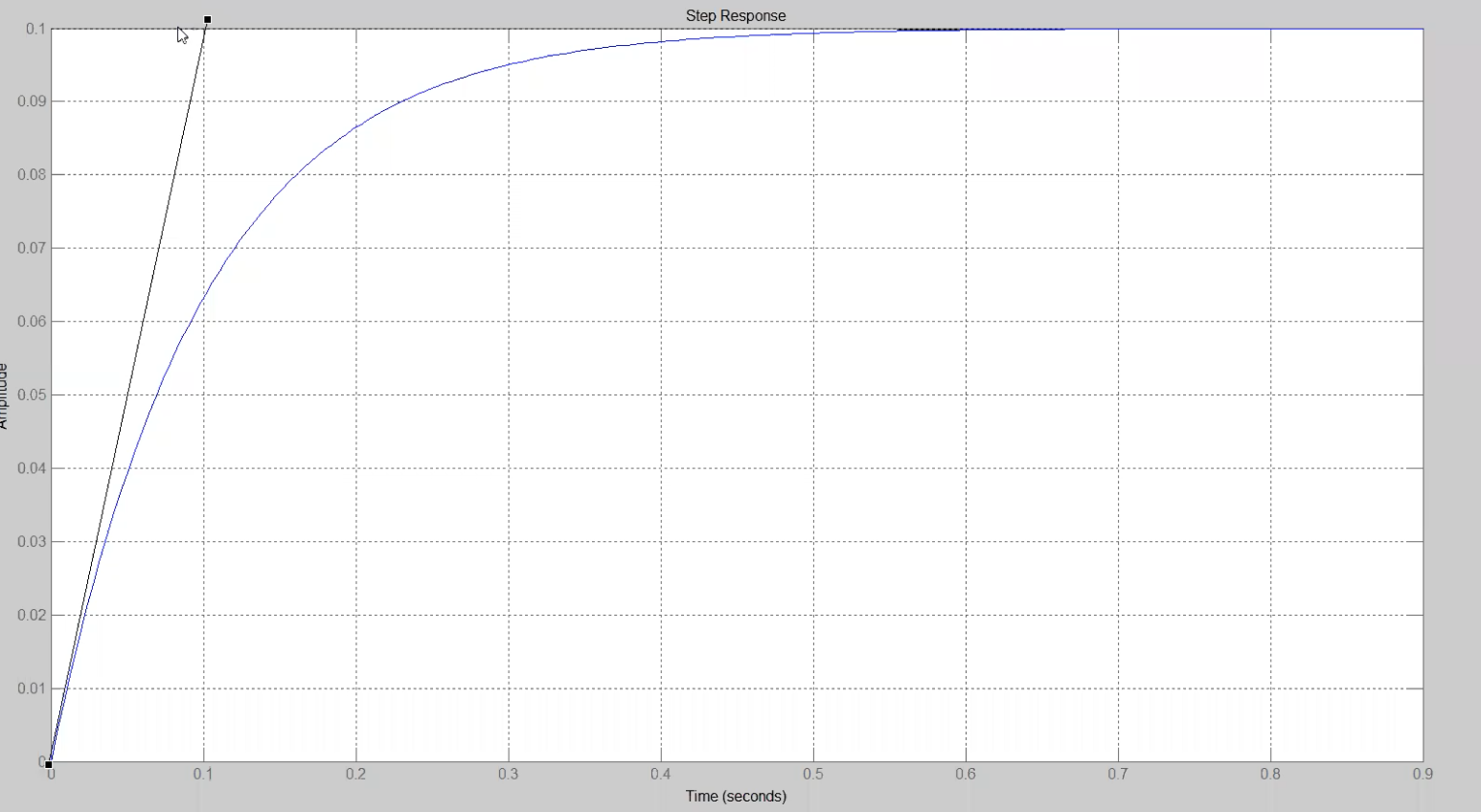
Formulazione del problema: arrivare alla FdT partendo da un grafico della risposta al gradino

Se ho questo grafico:

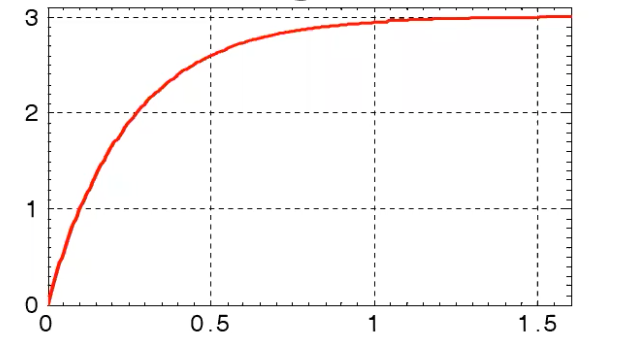
che sembra proprio la risposta al gradino di un sistema del primo ordine BIBO-stabile, posso facilmente scrivere la sua funzione di trasferimento osservando i parametri caratteristici:

• il suo valore di regime $y_{\infty }$ è $3$ $⟹$ dato che l’ingresso era il gradino unitario $\overline{u}=1$ e ho $y_{\infty }=K\overline{u}$, $K=3$.
• la risposta arriva a $0.95\cdot 3=2.85$ in $t=0.75⟹\tau =0.25$;
  • metodo alternativo: la risposta arriva a $0.63\cdot 3=1.89$ in $t=0.25$

In MATLAB, tutto questo si può fare con:

• 
• 
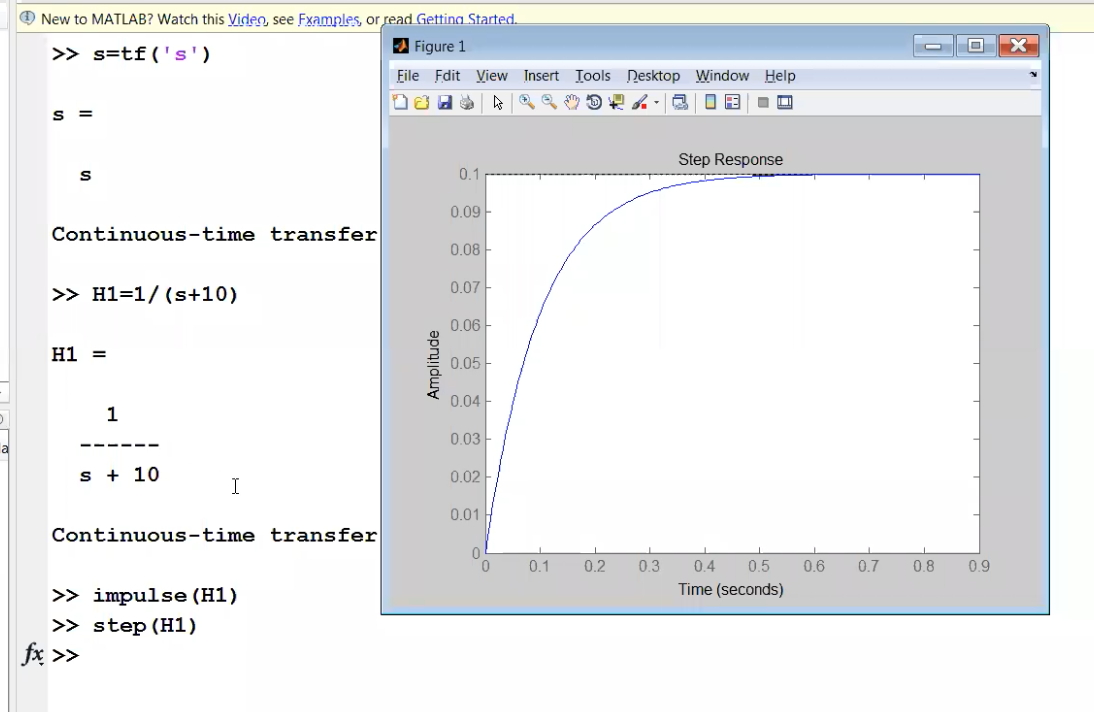
• ltiview fa aprire una GUI in cui possiamo importare le transfer functions e permette di calcolare i parametri caratteristici.
  • dai menu della GUI puoi vedere risposte ad impulso, gradino, fare i diagrammi di Bode in modulo e fase
  • tasto destro > Characteristics >
    • Steady State ti dice il valore finale
    • Rise Time ti dice il $t_r$
    • Settling Time ti dice il tempo di assestamento al $2\%$, si può cambiare da tasto destro > Properties > Options.
    • se vuoi fare lo stronzo, puoi anche cambiare da Options il comportamento di Rise Time in modo che ti indichi il tempo dallo $0\%$ al $63\%$ (ovvero, anche se lui lo chiama ancora Rise Time, la costante di tempo). Come pure definire il Settling Time al $37\%$ si può ottenere sempre la costante di tempo.
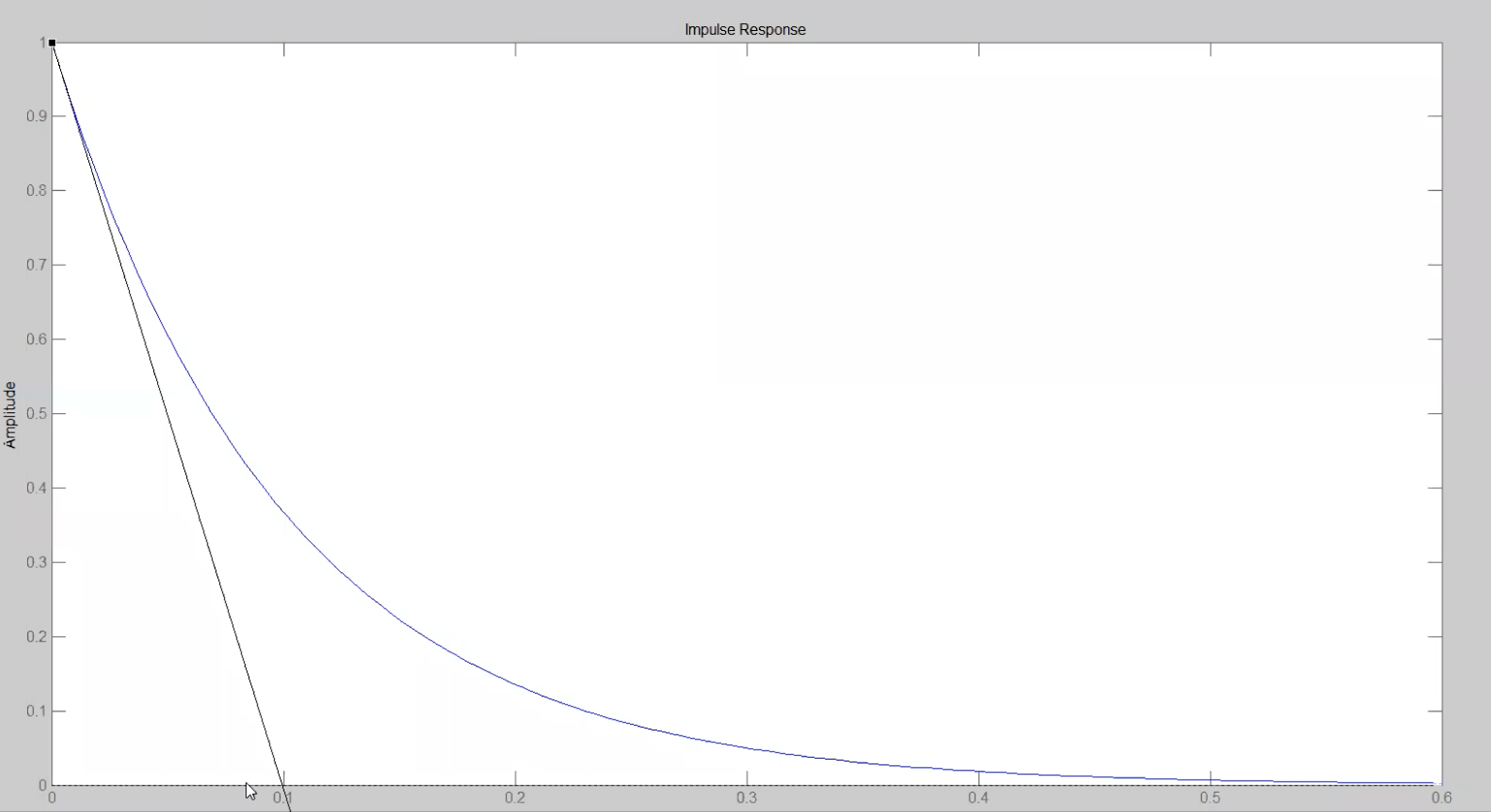
  • La costante di tempo si può anche calcolare graficamente, cioè plottando o la risposta al gradino o la risposta all’impulso e, senza ltiview, direttamente dalla finestra del grafico facendo Insert > Line, metti una retta che sia tangente al grafico della risposta nel punto ad ascissa nulla;
    • se usi il grafico della risposta all’impulso, vedi l’ascissa del punto di intersezione tra la retta costante del valore di regime $y_{\infty }$ e la tangente che hai disegnato; quella è la costante di tempo
      • 
    • se usi il grafico della risposta al gradino, vedi l’ascissa del punto di intersezione tra l’asse dei tempi e la tangente che hai disegnato; quella è la costante di tempo
      •