TAR18.Retroazione statica dello stato

Un sistema SISO, LTI e TC di base fa quello che gli pare, in base a
$\dot{x}(t)=Ax(t)+Bu(t)$
La sua risposta potrebbe avere sotto/sovra elongazioni non accettabili, essere troppo lenta a rispondere al cambiamento del segnale in input, oscillare, ecc.
È quindi necessario regolare il comportamento del sistema, modificando il suo comportamento e, volendo, anche limitandolo in un range di funzionamento (es. anche se l’input aumenta di tanto, e l’output dovrebbe aumentare a sua volta, invece fornisci un output all’interno di un range, sbattendo su un upper bound. Così non bruci tutto).
Per regolare il sistema è necessario costruire uno schema di componenti “intorno” al sistema stesso, e questo schema è quello della retroazione: infatti è necessario che il sotto-sistema di controllo si basi sullo stato corrente del sistema per dedurne quali micro-aggiustamenti fare.
I micro-aggiustamenti saranno tradotti nella variazioni del segnale di ingresso al sistema, che a questo punto non sarà direttamente la variabile di ingresso che si usava prima.
Infatti sarà il sotto-sistema di controllo a produrre i segnali di ingresso al sistema vero e proprio, in base alla retroazione e alla legge di controllo
$u(t)=\alpha r(t)-Kx(t)$

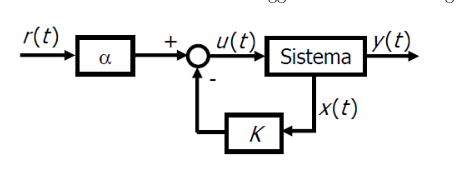
Allora $u(t)$, in questo scenario, non è più l’ingresso del sistema, che è $r(t)$; viene invece detto comando.
Il segnale $r(t)$, invece, è un riferimento e coincide sostanzialmente con “un andamento desiderato” di $y(t)$, quindi $y_{\text{des}}(t)$.
Il sotto-sistema di controllo, quindi, è in grado (perlomeno, idealmente lo sarebbe) di forzare il sistema originale ad inseguire con la propria uscita un andamento ideale.

Esempio

Voglio che la mia auto non sbandi in curva. Tramite le informazioni che ottengo in ogni momento dai sensori di stabilità, dal volante, dalle ruote, dalla velocità ecc. costruisco un segnale di riferimento, magari tramite un computer di bordo.
Allora il sotto-sistema di controllo del mio “sistema auto”, tramite la legge di controllo, costruisce uno o più “comandi” (es. comandi da dare all’ABS, ridurre la velocità, sterzare ecc.), segnali variabili, che comandino il “sistema auto” perchè, nel complesso, insegua un $r(t)$ che è la traiettoria che, idealmente, vorrei che la macchina seguisse.

$K$ è una matrice $p\times n$ di guadagni (pesi, coefficienti costanti di una combinazione lineare - da qui la definizione di retroazione statica, in contrapposizione ad una dinamica che non vedremo mai) che moltiplicano le variabili di stato, stessa cosa con $\alpha$ che è invece in $p\times q$ in modo che effettivamente esca poi $u$ di dimensione $p$ come al solito. Nel caso di un sistema con un solo ingresso, la matrice $K$ si riduce quindi ad un vettore riga.

Matematicamente, possiamo ricavare cosa succede effettivamente al sistema e come stimare l’uscita di questo “sistemone”, somma del sistema originale e del sotto-sistema di controllo.
Sostituendo l’espressione di $u(t)$ nelle equazioni del sistema:
$\dot{x}(t)=(A-BK)x(t)+B\alpha r(t)$
$y(t)=(C-DK)x(t)+D\alpha r(t)$
si nota che ciò che accade è una modifica in tempo reale della matrice di stato (da $A$ ad $A-BK$): questo sicuramente modifica il comportamento del sistema.
In particolare, modifica gli autovalori del sistema, i quali sappiamo bene come siano indicatori della stabilità interna del sistema: questo significa che possiamo anche forzare un sistema instabile a diventare stabile.

Assegnazione degli autovalori o legge di controllo

Sostanzialmente lo scopo di questa parte è: gli autovalori determinano il comportamento dinamico libero del sistema - cioè l’evoluzione libera dello stato, che a sua volta prende parte alla determinazione dell’uscita libera del sistema.
Se ti trovi un sistema davanti che non ti piace come si comporta (nella sua uscita), puoi modificarne gli autovalori.

In realtà non modifichi gli autovalori del sistema in sè, ma piuttosto inglobi il sistema in un sistema più grande, che presenta lo schema della retroazione e che nel complesso abbia gli autovalori che desideri (ecco perchè si dice assegnazione e non modifica o regolazione degli autovalori).
All’interno di questo sistema più grande c’è il tuo sistema originale, che ora ha come ingresso un segnale che viene determinato in ogni istante “spiando” l’uscita tramite la retroazione, in modo che al sistema originale arrivino sempre e solo ingressi che lo portino a produrre in uscita segnali noti e desiderati.

La condizione di raggiungibilità è quindi necessaria. Se un sistema è raggiungibile, possiamo sapere come un sistema si comporterà nella sua uscita (o nella sua evoluzione dello stato, che quindi tramite $y=Cx+Du$ mi da anche l’evoluzione dell’uscita) all’applicarsi di un dato ingresso (appena computato) - anche prima di “provare” a darlo in pasto al sistema e registrare l’uscita.
È un modo per fare una stima a priori. E se puoi fare questa stima a priori, allora puoi anche computare correttamente un ingresso che in ogni istante forzi il sistema a comportarsi come vuoi tu. Il senso è sempre quello.

Warning

Possibilità di errore nella computazione del comando
(nel senso che pur dando in pasto al sistema un comando computato apposta per far dare in output un certo segnale, il sistema comunque da in output un altra roba)

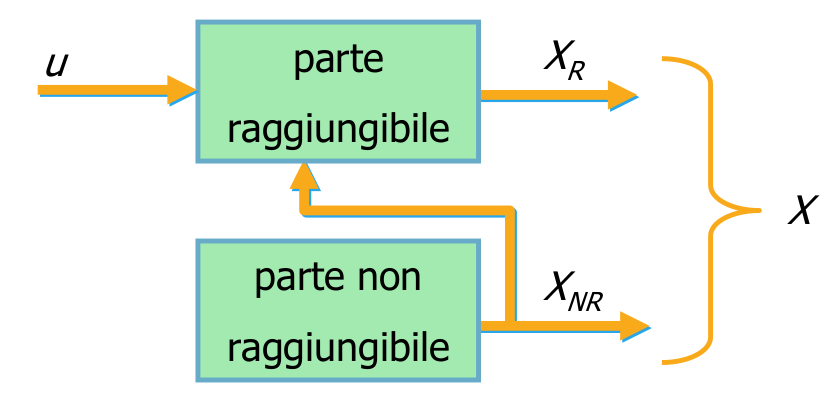
La parte non raggiungibile del sistema può influenzare l’uscita del sistema tanto quanto quella raggiungibile, quindi è possibile che il sistema non risponda come previsto ad un certo input. La certezza che funzioni tutto la hai solo se il sistema è completamente raggiungibile.

Il problema dell’assegnazione degli autovalori mediante l’applicazione della retroazione statica dello stato ammette soluzione se e solo se la coppia di matrici $(A,B)$ soddisfa la condizione di completa raggiungibilità (puoi dire subito che il sistema è completamente raggiungibile se lo hanno scritto nell’esercizio già in forma canonica di raggiungibilità, else: devi controllare con MATLAB il rango della $M_r$).

Altrimenti la legge di controllo modificherebbe solo $\text{rank}(M_r)$ autovalori (quelli che sono corrispondenti alla parte raggiungibile del sistema). Potrebbe anche andare bene così in certi sistemi, ma sicuramente non potresti risolvere problemi legati agli autovalori non raggiungibili. Ad esempio, se uno di quegli autovalori non raggiungibili è associato ad un modo naturale divergente, non sarà possibile stabilizzare il sistema con questo metodo.

infatti nell’esempio:

Per capire quali sono gli elementi di $K$ (trovare la legge di controllo) intanto scrivi le equazioni del sistema controllato in funzione degli elementi di $K$ e poi eguagli il polinomio caratteristico che hai trovato al polinomio caratteristico che avresti se il sistema avesse esattamente gli autovalori dati (considera che il polinomio caratteristico è un polinomio normale che si annulla negli autovalori, quindi per esempio se desideri che gli autovalori siano $-2$ e $-3$, il polinomio caratteristico sarà $(\lambda +2)(\lambda +3)$).

Regolazione sull’uscita

È possibile trovare, dato un sistema LTI TC SISO a cui è applicata una retroazione statico dello stato, con $r(t)=\overline{r}$ costante, calcolare uno stato costante $\overline{x}$ e un’uscita costante $\overline{y}$ tali che $\overline{y}=\overline{r}$? (= trovare una legge di controllo che lo permetta)
$\overline{x}=-(A-BK{)}^{-1}B\alpha \overline{r}$
$\overline{y}=[-(C-DK)(A-BK{)}^{-1}B+D]\alpha \overline{r}$ e affinchè $\overline{y}=\overline{r}$ deve risultare
$[-(C-DK)(A-BK{)}^{-1}B+D]\alpha =1$
e infine:
$\alpha =[-(C-DK)(A-BK{)}^{-1}B+D{]}^{-1}$