Introduzione
Innanzitutto quando parliamo di sistemi del secondo ordine quello di cui parliamo sono i sistemi la cui FdT ha due poli al denominatore.
- , per cui abbiamo che il numeratore può essere una costante oppure un polinomio di I grado.
- Nei sistemi di II ordine, dato che ci possono essere due poli, questi possono anche essere complessi coniugati, cosa che non succedeva nel caso di sistemi del I ordine.
- Inoltre, la risposta all’impulso per sistemi del II ordine la ignoreremo: si parlerà solo di risposta al gradino.
Qui abbiamo sempre
quindi anche
e
(perchè si, stiamo ancora considerando il caso in cui il sistema parte a riposo, quindi abbiamo solo una risposta forzata).
Due poli reali e distinti
Abbiamo
con ed entrambi .
Allora:
Questa si può scomporre in fratti semplici e antitrasformare come:
Questo è uno di quei casi in cui col cavolo che so graficare a colpo sicuro, quindi uso il teorema del valore iniziale e del valore finale dove posso.
- il teorema del valore iniziale vale sempre, perchè sicuramente la funzione è strettamente propria, e mi esce
- il teorema del valore finale è valido solo se e (sono reali quindi la loro parte reale è tutto ciò che sono, va bene scrivere così) (cioè è BIBO-stabile), e mi da
Posso scrivere una costante di tempo equivalente, ma non posso calcolarla facilmente; posso ottenerne un’approssimazione, immaginando una costante di tempo associata ad ogni polo e sommandole:
(Questa approssimazione è tanto migliore più sono distanti tra loro i poli del sistema).
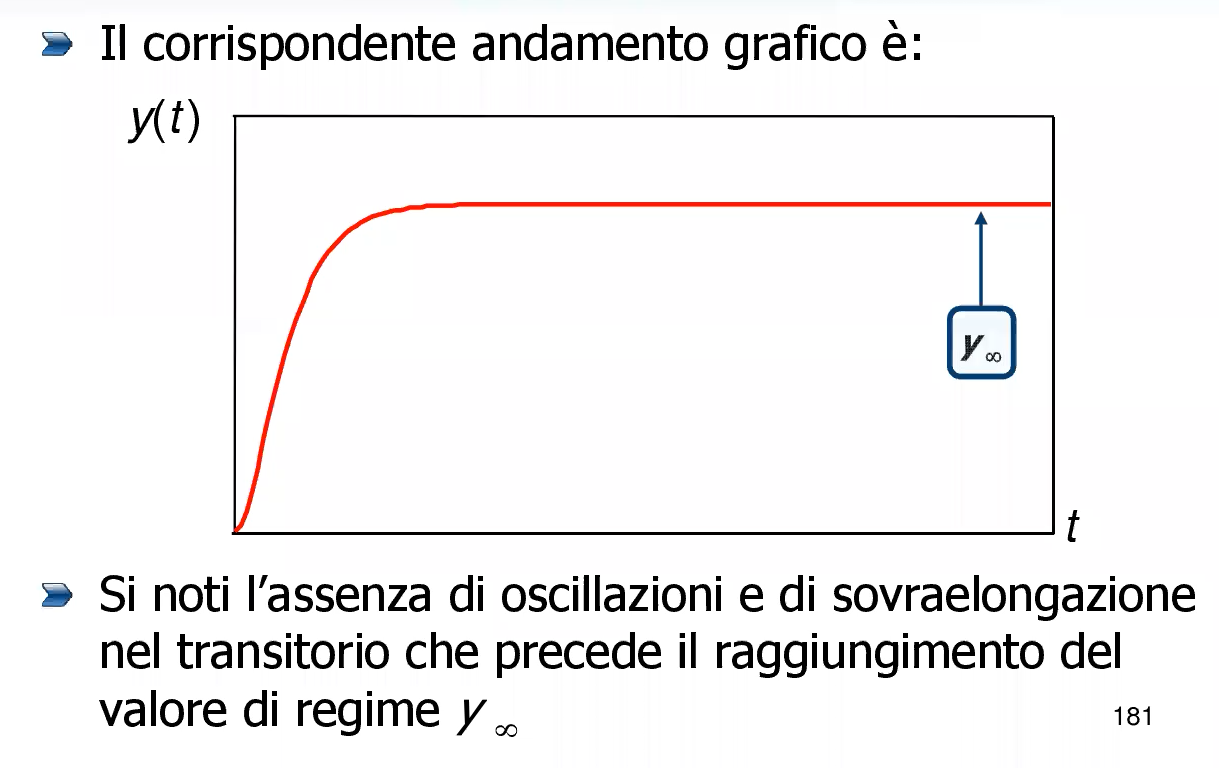
Se poi uno vuole, può effettivamente graficare o comunque studiare meglio questa funzione per capirne l’andamento oltre che ai punti iniziale e finale, che sono di per sè simili al caso del sistema di I ordine.
Si ottiene anche un grafico molto simile alla convergenza esponenziale della risposta al gradino di un sistema di I ordine, tuttavia c’è una sostanziale differenza: in il segnale parte con una tangente orizzontale, quindi ha un punto di flesso.
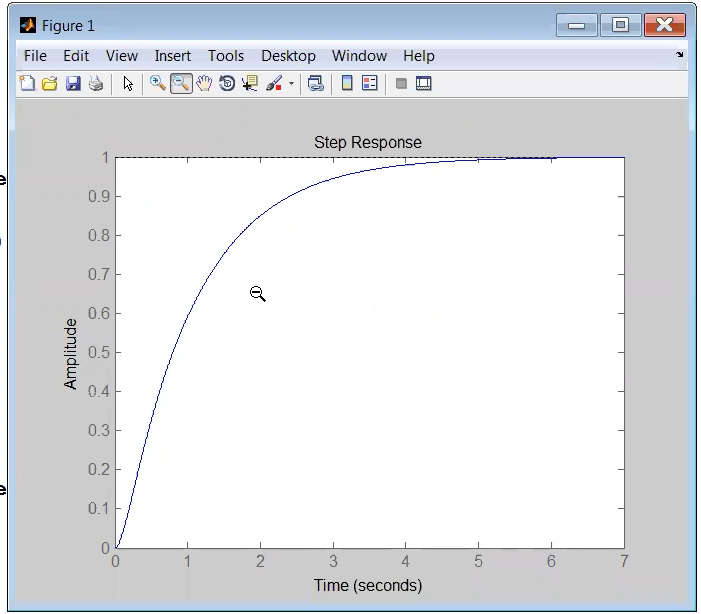
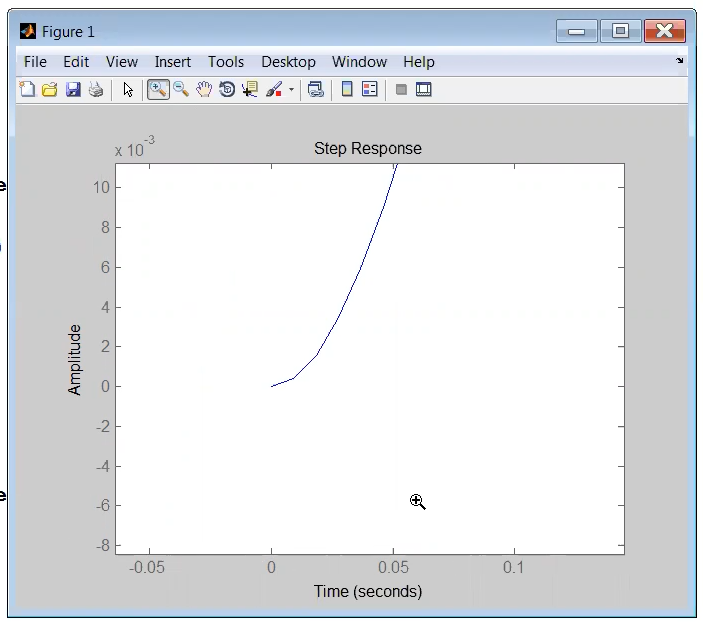
In verità dato che è così simile ad un sistema del I ordine, possiamo perfino calcolarci la costante di tempo equivalente su MATLAB come se fosse di primo ordine, cioè con il Rise Time da al , per esempio.
In effetti, la risposta che questo sistema ci da è veramente tanto simile alla risposta (in particolare, sono entrambe monotone crescenti e convergenti) che ci darebbe un sistema di I ordine con la stessa costante di tempo (per provarlo basta scrivere una funzione di trasferimento in forma di Bode mettendo la ).
Due poli reali e distinti e uno zero reale
Se la FdT ha forma
con distinti e non nulli, allora
che antitrasformando diventa
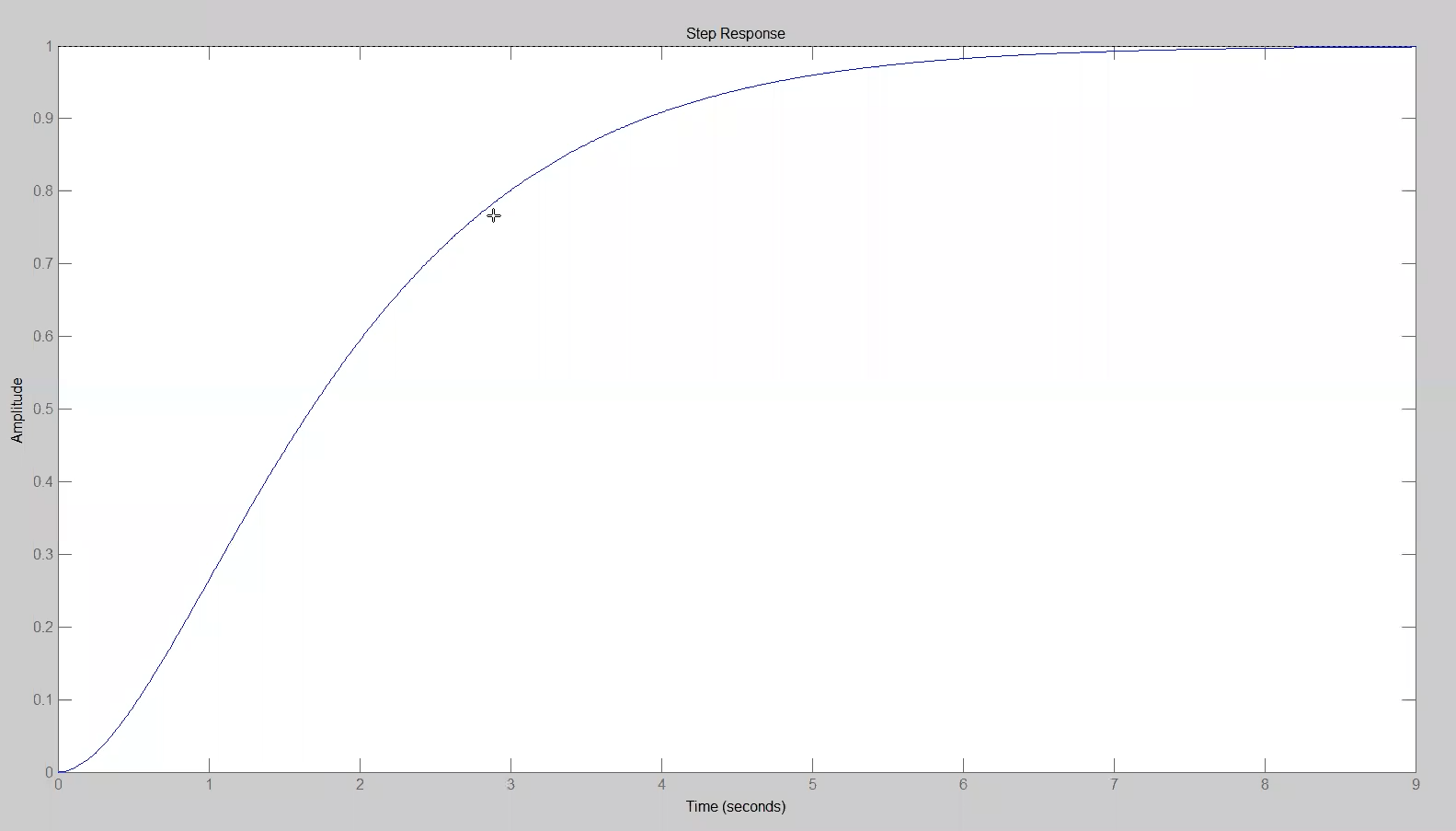
Se non ci sono sotto o sovra elongazione, vedi sotto, ha sempre un grafico dello stesso tipo di prima, una specie di esponenziale convergente ma che schiribissa alla partenza
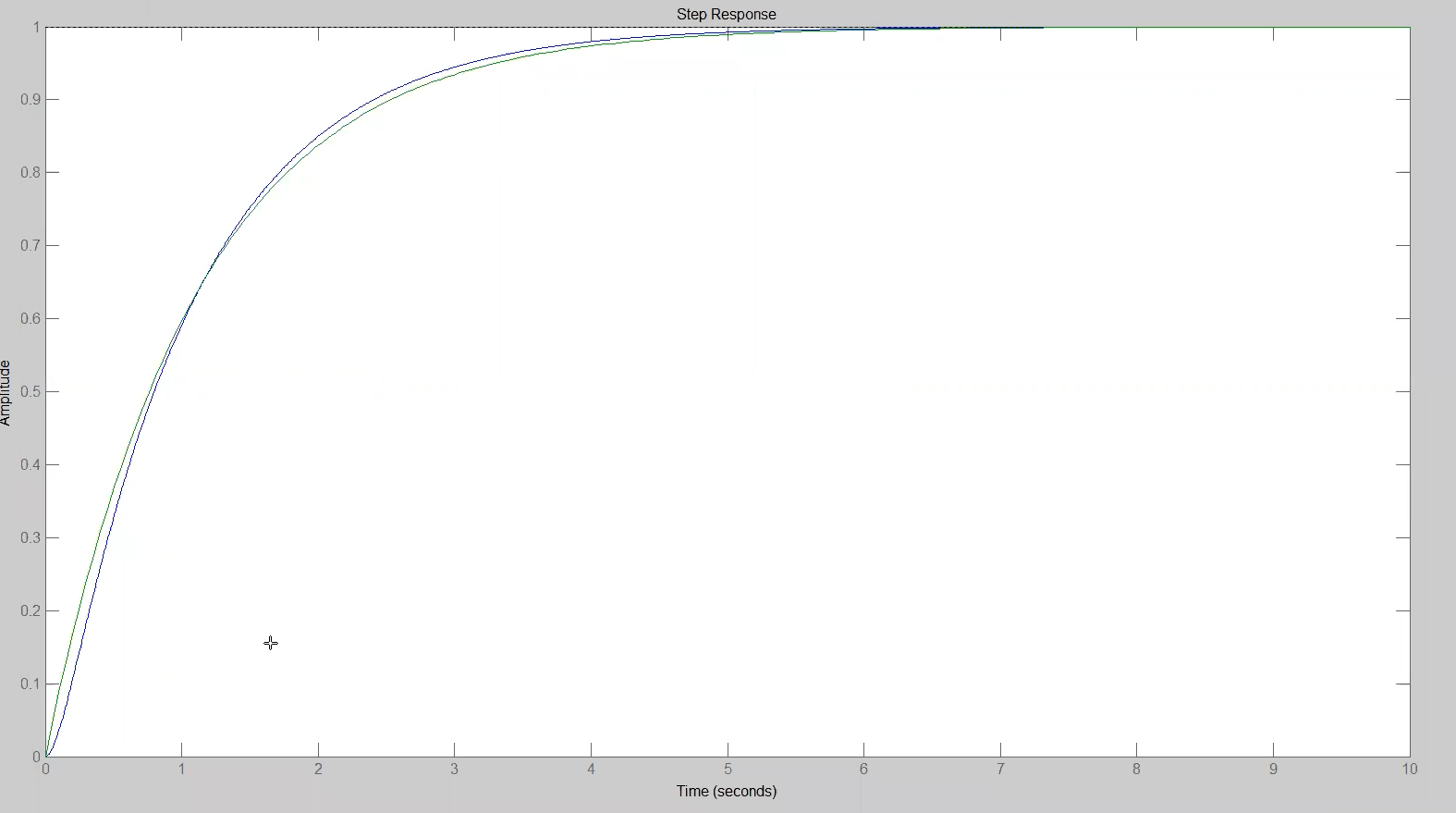
Variando notiamo che la risposta del sistema è sempre più “veloce” (raggiunge prima il valore ) quanto più è vicino allo .
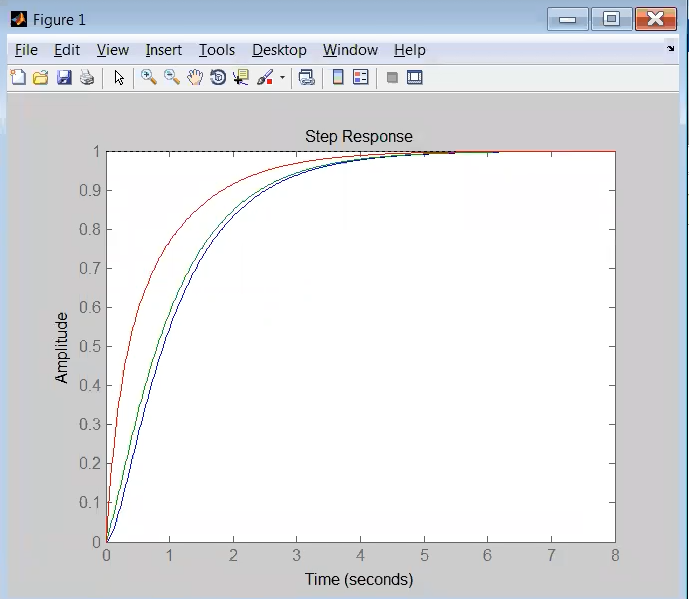
In effetti, possiamo approssimare la costante di tempo immaginando anche una costante di tempo associata allo zero e scrivendo:
La costante di tempo non ha senso se ci sono elongazioni, se ho capito bene.
Notiamo però che a seconda della posizione dello zero rispetto ai poli e a possono verificarsi i fenomeni di:
- un cazzo di niente se lo zero si trova a sinistra del polo a modulo minore (e puoi calcolare la costante di tempo equivalente di un sistema di primo grado molto simile) - al più, più lo zero vicino è in modulo allo più la risposta è veloce
- sovra-elongazione se lo zero si trova tra il polo a modulo minore e ; in questo caso con
ltiviewmi viene facile calcolare la sovra-elongazione (distanza rispetto al valore di regime) e il valore di picco. Un valore dello zero più vicino in modulo a mi fa avere una sovra-elongazione maggiore - sotto-elongazione se lo zero si trova a destra dello (è positivo). Anche qui l’effetto è maggiore minore è la differenza tra lo zero e lo . Questa non è proprio semplice da vedere con MATLAB perchè non ho il “valore di picco” ma ho un picco al contrario. Magari posso fare il picco di
absdel vettore… boh.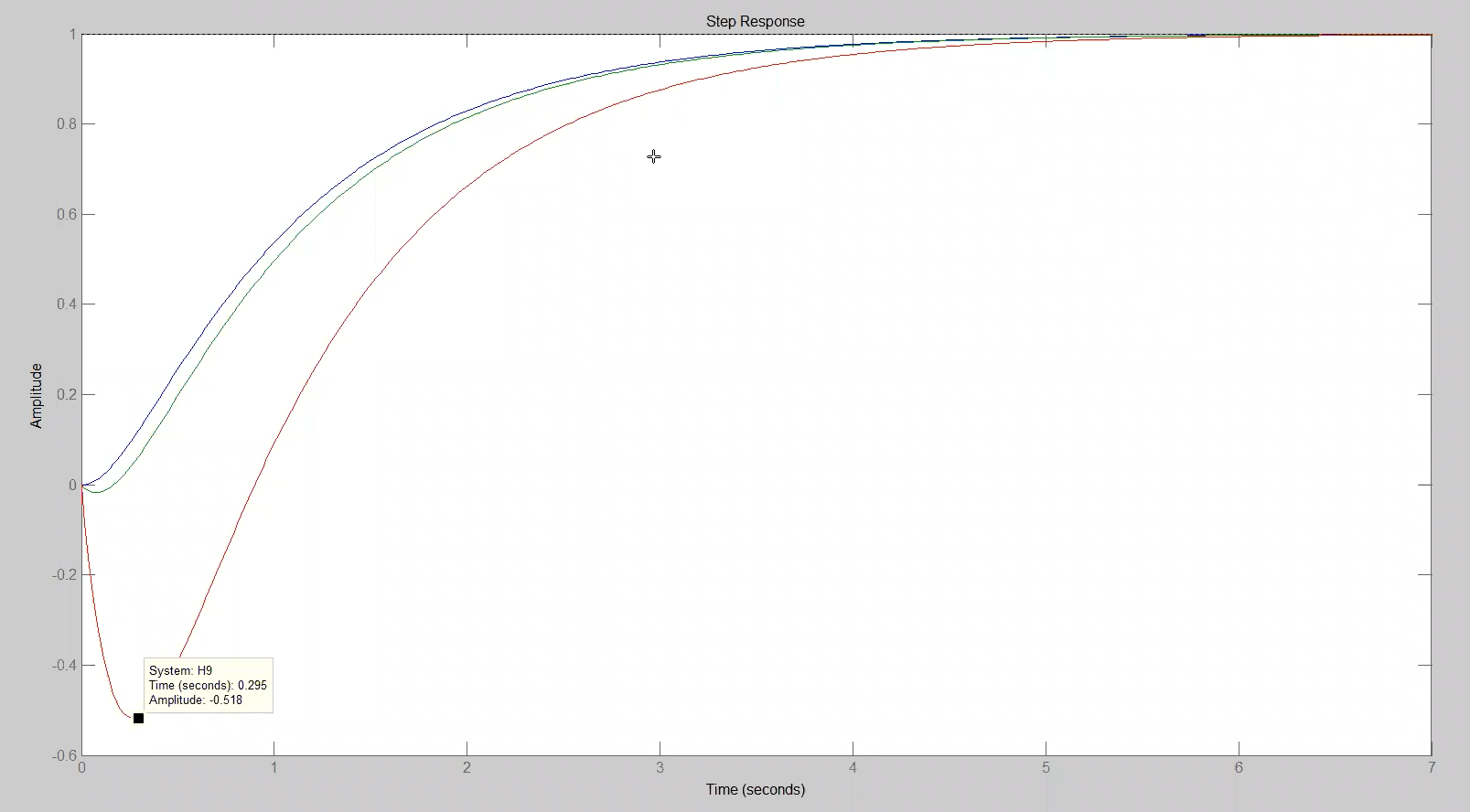
- Esempio: tirando la cloche di un aereo per tirarlo su ottieni sempre un “undershoot” di questo tipo (FdT tra movimento della cloche e altezza del velivolo) - quindi occhio perchè prima affossi un pochino il muso e poi ti alzi. Se provi a fare sta cosa troppo vicino ad un ostacolo sicuro ti schianti.
Due poli complessi coniugati
Una FdT con due poli complessi coniugati si può scrivere in forma zeri e poli generalizzata a polinomi aventi radici complesse, quindi in forma
con
- guadagno,
- pulsazione naturale (della coppia di complessi coniugati),
- smorzamento (della coppia di complessi coniugati)
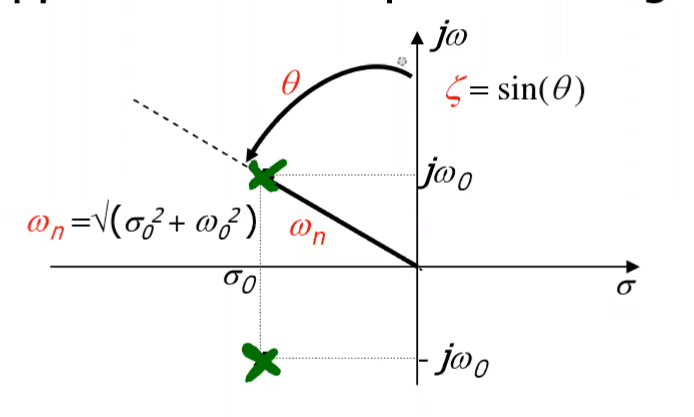
Definiamo allora una costante di tempo come .
La risposta la calcoliamo dall’antitrasformata di come prima, e a sto giro faccio copia e incolla prima di uccidermi:
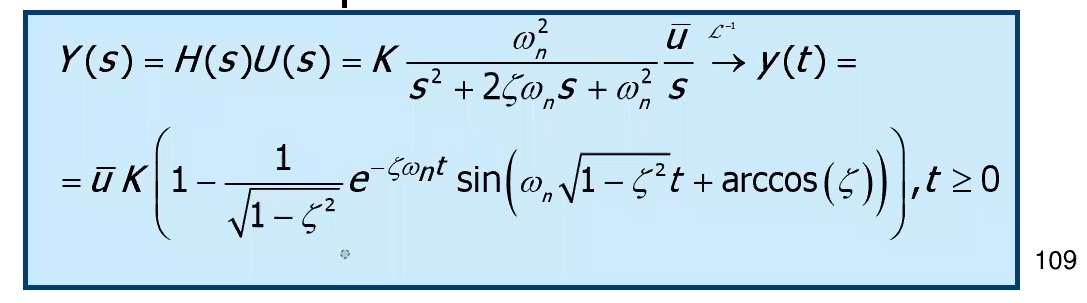
Cioè abbiamo
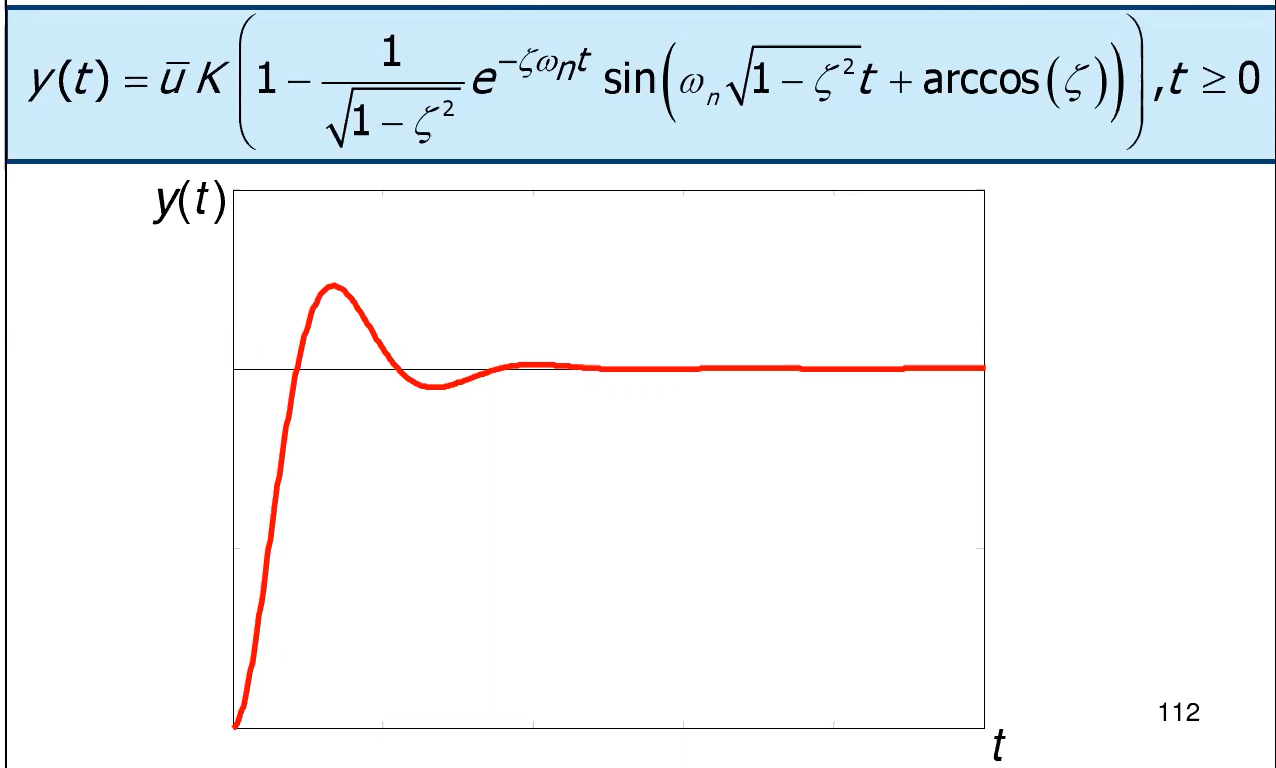
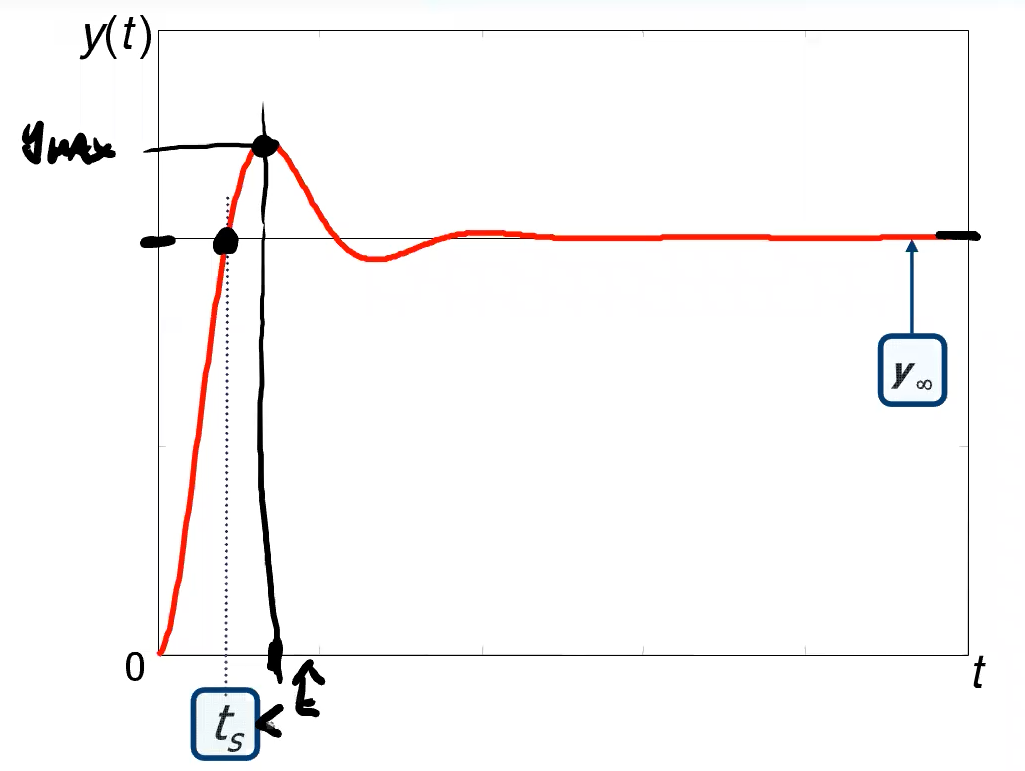
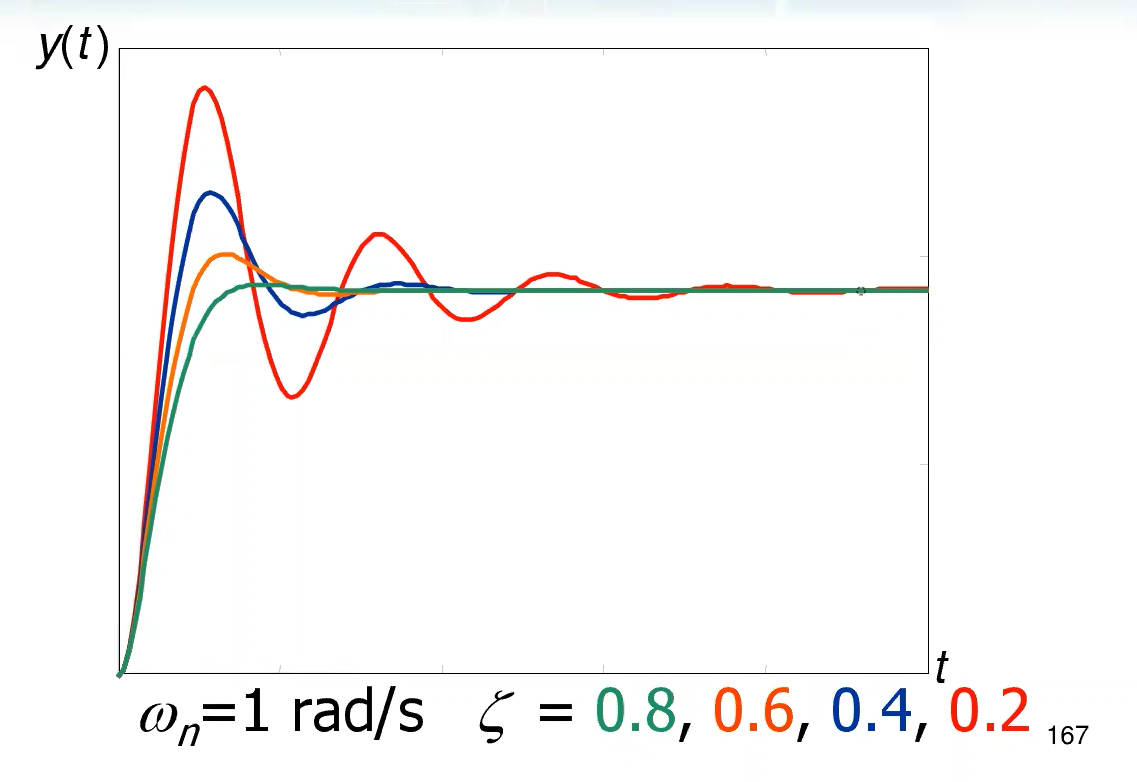
Presenta sia sovra-elongazione sia sottoelongazione, inoltre dopo questi due picchi continua ad oscillare, fermandosi dopo poco dato l’inviluppo esponenziale. La risposta quindi non è assolutamente monotona.
I parametri tipici sono:
- valore di regime , calcolabile con il teorema del valore finale (sì, vale se poli a parte reale strettamente negativa) - il valore finale è
- valore di picco y_\max che otteniamo da
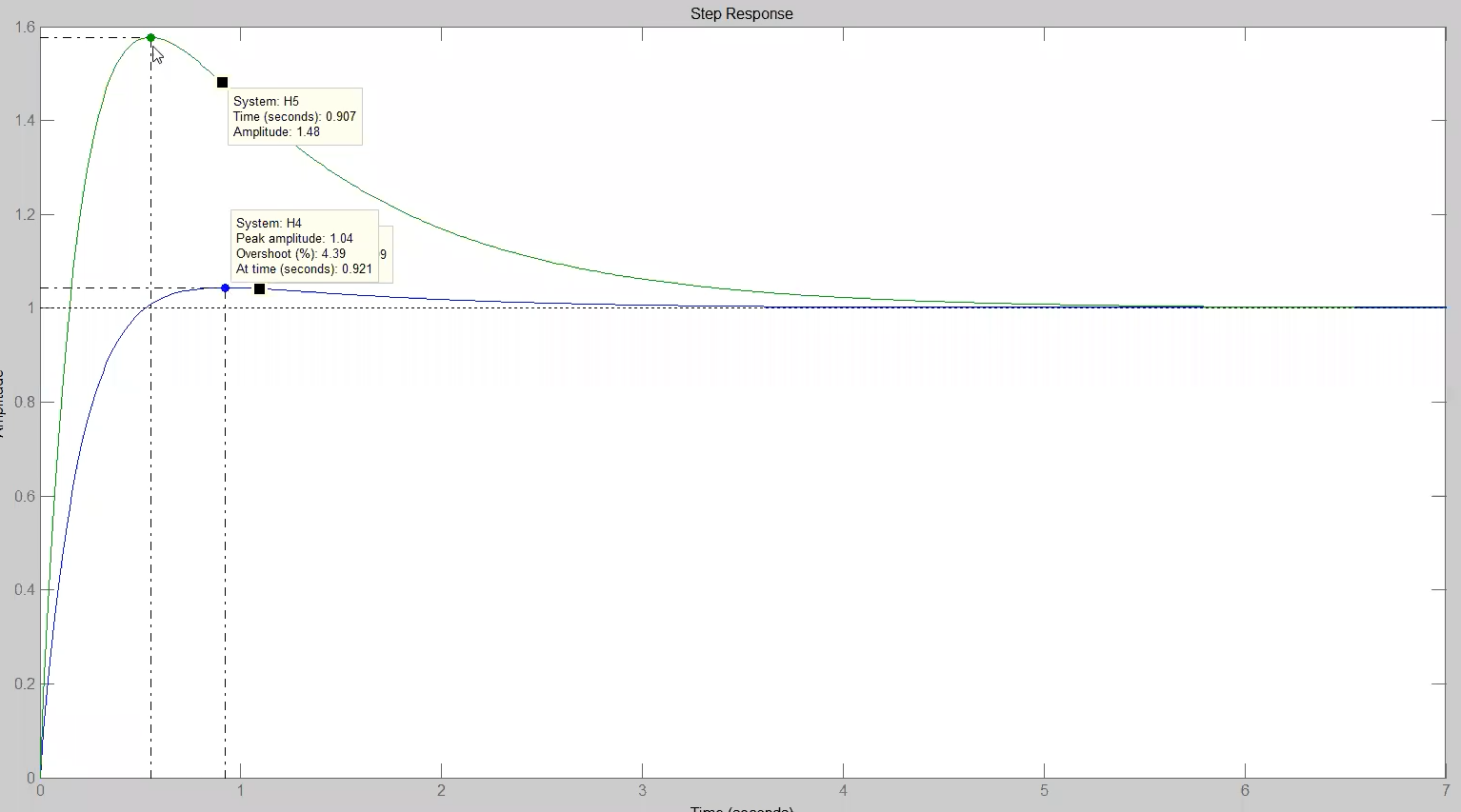
ltiview, sempre plottando, ed è ovviamente - sovraelongazione massima \hat{s}=(y_\max-y_\infty)/y_\infty tra e , si può anche considerare in termini percentuali
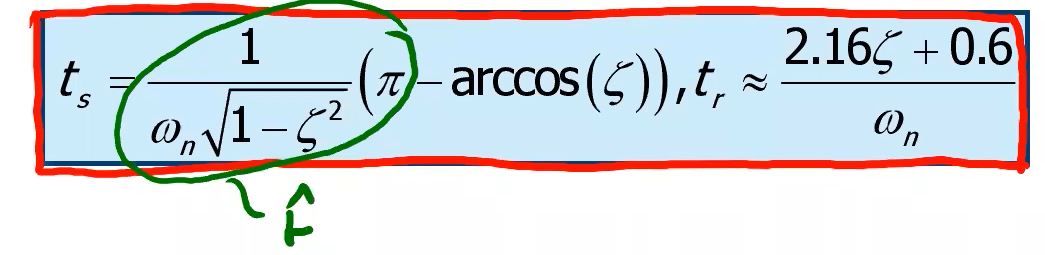
- tempo di picco , tempo tale per cui y(\hat{t})=y_\max
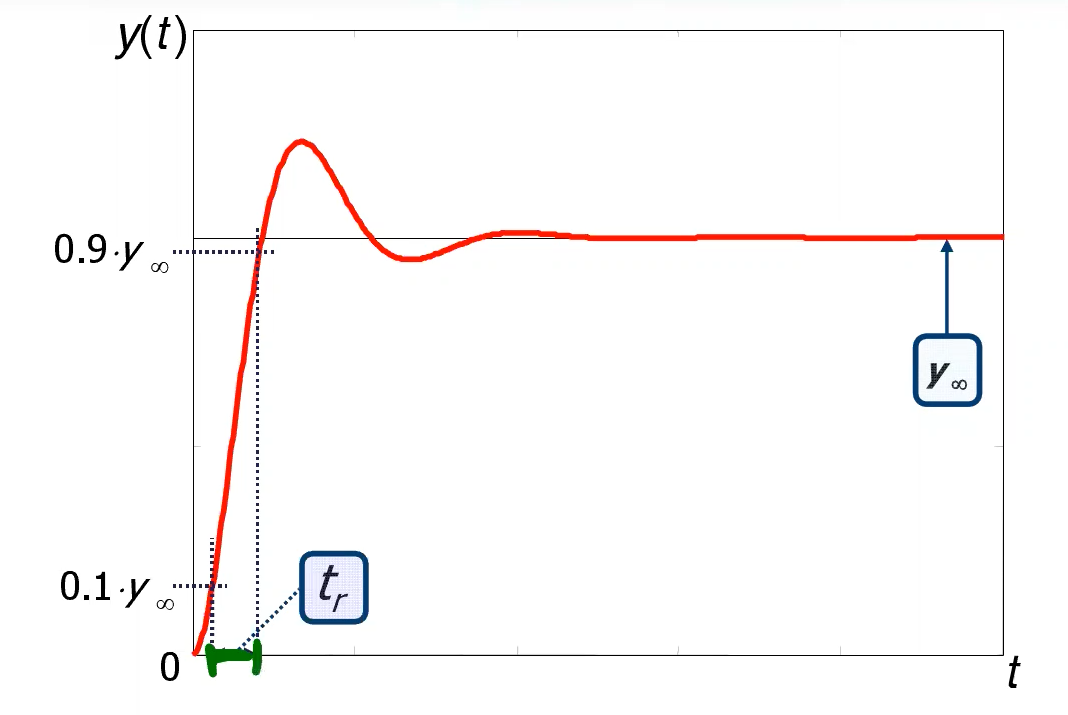
- tempo di salita , primo istante temporale in cui la risposta raggiunge il valore di regime , anche se dopo la risposta cresce per arrivare al picco (questo si può definire sempre)
- rise time dal al (solo per sistemi del secondo ordine con risposta oscillante, quindi con poli complessi coniugati si può fare - non si può per quelli del secondo ordine non oscillanti)
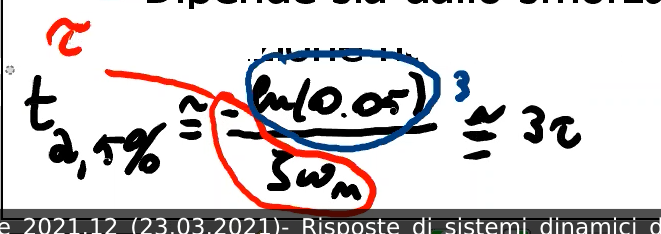
- tempo di assestamento al - tempo perchè la risposta differisca dal valore finale di non più del . (sarebbe il rise time da al ).
Ci sono anche formule che ti permettono di calcolare alcuni di questi parametri senza plottare, per cui la sovraelongazione massima dipende unicamente dallo smorzamento, mentre tempo di picco sia da smorzamento che da pulsazione naturale (valgono solo nel caso di questi valori complessi coniugati, non nel caso di secondo ordine quelli di prima coi poli reali):

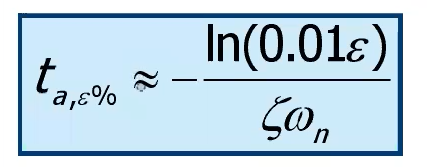
Vediamo che al variare del solo smorzamento abbiamo questo tipo di effetto sulla risposta (più oscillazioni):
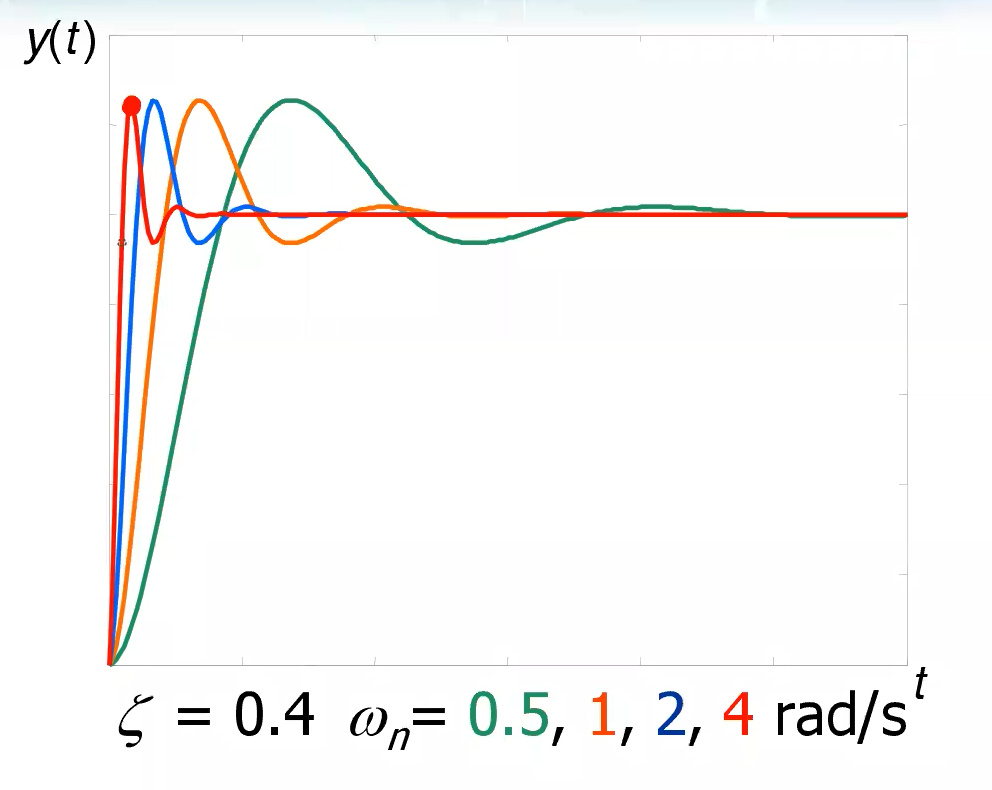
Al variare della sola pulsazione naturale, invece, le elongazioni restano uguali ma si velocizza la risposta:
Caso