IND02a.Diagrammi per l’analisi in frequenza dei sistemi in retroazione

I principali diagrammi che utilizzeremo per rappresentare e studiare più “agevolmente” la risposta in frequenza di un sistema sono:

• I diagrammi di Bode
• I diagrammi polari
• I diagrammi di Nyquist
• I diagrammi di Nichols

Diagrammi di Bode

Considerando una funzione di trasferimento di un sistema nel dominio della frequenza $G(s)$ e ricordando che la variabile $s$ del dominio di Laplace è una variabile complessa, $s=j\omega$ con $\omega$ detta pulsazione, possiamo pensare di graficare $G(j\omega )$ in vari modi, sfruttando le varie rappresentazioni possibili di un numero complesso.
Ad esempio, possiamo pensare di scrivere $G(s)$ nella sua rappresentazione in modulo e fase e graficare separatamente i due parametri, su due grafici diversi che abbiano come ascissa la pulsazione.
Normalmente useremmo una scala lineare per entrambi i grafici e per entrambi gli assi di ogni grafico (grafico naturale). Tuttavia, tale rappresentazione non è comoda per avere un colpo d’occhio. Allora noi faremo un passaggio intermedio, effettuando la conversione del modulo da unità naturali a decibel tramite $20{\log }_{10}(G(s))$ e graficheremo quindi la pulsazione in scala logaritmica.
La fase la manterremo in gradi, ma anche nel grafico della fase useremo la scala logaritmica per la sola ascissa.

Info

Prodotto di funzioni di trasferimento (blocchi in cascata)
Un altro vantaggio che traiamo nell’utilizzare la rappresentazione in modulo e fase, in particolare col modulo in decibel (notare che è una forma logaritmica) è che il prodotto di funzioni di trasferimento, ad esempio utile per calcolare la funzione di trasferimento complessiva di una serie di blocchi in cascata, diventa più semplice:

• il modulo di $G_1\cdot G_2$ è la somma dei moduli di $G_1$ e $G_2$
• la fase di $G_1\cdot G_2$ è la somma delle fasi di $G_1$ e $G_2$

Così facendo avremo disegnato i diagrammi di Bode di modulo e fase di $G(s)$.

Per costruire manualmente i diagrammi di modulo e fase, è necessario memorizzare quali siano i contributi in termini di modulo e fase di $4$ fattori fondamentali. Le funzioni di trasferimento che ci capiterà di dover graficare si potranno sempre riscrivere come composizioni di questi fattori, tramite manipolazioni algebriche. Sono scritti elevati alla $-1$ perchè infatti la trattazione successiva suppone di trovarsi questi fattori al denominatore della funzione di trasferimento. Se si trovano al numeratore poi vediamo cosa succede.

I fattori fondamentali sono:

1. $K$
   1. è un fattore di tipo guadagno
   2. il DdB del suo modulo è una retta costante di valore $20{\log }_{10}K$
   3. il DdB della sua fase è una retta costante del valore $0K>0,-180K<0$
2. $s^{-1}$
   1. è un fattore integratore (è un polo in $0$ per la funzione di trasferimento)
   2. consideriamo piuttosto il fattore $K{s}^{-1}$ così da analizzarne due insieme
   3. il DdB del suo modulo è una retta di pendenza $-20$ dB/decade e passante per i punti $(1,20{\log }_{10}K)$ e $(|K|,0)$
   4. il DdB della sua fase è una retta costante a $-90°$
3. ${\left(1-\frac{s}{\lambda }\right)}^{-1}$
   1. la funzione di trasferimento ha un polo reale in $\lambda$
   2. per considerare i suoi contributi al diagramma di Bode della funzione, consideriamo la pulsazione normalizzata $\Omega =\omega /|\lambda |$
   3. il DdB (con $\Omega$ per ascissa) del suo modulo è
      1. in BassaFrequenza (AF) ($\Omega <<1⟺\omega <<|\lambda |$): costante a $0$ dB
      2. in AltaFrequenza (BF) ($\Omega >>1⟺\omega >>|\lambda |$): retta con pendenza di $-20$ dB/decade
      3. nel punto centrale ($\Omega =1⟺\omega =|\lambda |$): il modulo è di $-3$ dB (quindi nel punto centrale il modulo è attenuato del $50\%$)
      4. Se si vuole tracciare un grafico “asintotico”, il suo contributo è una spezzata che ha valore $0$ fino al punto centrale e scende di pendenza $-20$ dB/decade da lì in poi.
   4. il DdB (con $\Omega$ per ascissa) della sua fase è
      1. in BassaFrequenza (AF) ($\Omega <<1⟺\omega <<|\lambda |$): costante a $0°$
      2. in AltaFrequenza (BF) ($\Omega >>1⟺\omega >>|\lambda |$): costante a $-90°$ per polo stabile, $90°$ per polo instabile
      3. nel punto centrale ($\Omega =1⟺\omega =|\lambda |$): la fase è di $-45°$ per polo stabile, $45°$ per polo instabile
      4. Se si vuole tracciare un grafico “asintotico”, il suo contributo è una spezzata che ha valore $0$ fino ad una decade prima del punto centrale, poi una retta di pendenza $\pm 45°$/decade fino ad una decade dopo il punto centrale, poi ha valore $\pm 90°$.
4. ${\left(1+\frac{2\zeta }{{\omega }_n}s+\frac{s^2}{{\omega }_n^2}\right)}^{-1}$
   1. la funzione di trasferimento ha due poli complessi coniugati, di pulsazione naturale ${\omega }_n$ e smorzamento $\zeta$ (rivedi qui in caso di dubbi)
   2. per considerare i suoi contributi al diagramma di Bode della funzione, consideriamo la pulsazione normalizzata $\Omega =\omega /{\omega }_n$
   3. Ipotesi: $\zeta \ne 0$
      1. il DdB (con $\Omega$ per ascissa) del suo modulo è
         1. in BassaFrequenza (BF) ($\Omega <<1⟺\omega <<{\omega }_n$): costante a $0$ dB
         2. in AltaFrequenza (AF) ($\Omega >>1⟺\omega >>{\omega }_n$): retta con pendenza $-40$ dB/decade
         3. nel punto centrale ($\Omega =1⟺\omega ={\omega }_n$): il modulo è pari a $20{\log }_{10}\left(\frac{1}{2|\zeta |}\right)$
         4. Se si vuole tracciare un grafico “asintotico”, il suo contributo è quasi come quello del polo in $0$ ma con pendenza doppia, e potrebbe presentare un massimo (un punto di flesso a tangente verticale, un punto di non derivabilità a cuspide)(effettivamente è un picco, detto picco di risonanza) in corrispondenza di una specifica pulsazione ${\omega }_r$. Questo massimo quindi “alza” il grafico intorno a lui.
            1. Il picco esiste se $|\zeta |<1/\sqrt{2}\approx 0.707$
            2. ${\omega }_r={\omega }_n\sqrt{1-2{\zeta }^2}$
               1. quindi ${\omega }_r\ne {\omega }_n$ e anzi la sua posizione dipende dagli specifici poli
            3. $M_r=M({\omega }_r)=\frac{1}{2|\zeta |\sqrt{1-{\zeta }^2}}>1$
      2. il DdB (con $\Omega$ per ascissa) della sua fase è
         1. in BassaFrequenza (BF) ($\Omega <<1⟺\omega <<{\omega }_n$): costante a $0°$
         2. in AltaFrequenza (AF) ($\Omega >>1⟺\omega >>{\omega }_n$): costante a $-180°$ per polo stabile ($\zeta >0$), $180°$ per polo instabile ($\zeta <0$)
         3. nel punto centrale ($\Omega =1⟺\omega ={\omega }_n$): la fase è di $-90°$ per polo stabile, $90°$ per polo instabile
         4. Se si vuole tracciare un grafico “asintotico”, il suo contributo ha un asintoto orizzontale sinistro a $0$, uno destro a $\pm 180$ e intorno al punto centrale schiribissa come una $S$ al contrario in modo da avere nel punto centrale il $\pm 90$. L’ampiezza dello schiribisso, così come l’ampiezza della zona vicina al punto di risonanza che si alzava, dipende dal modulo dello smorzamento.
   4. Caso particolare: $\zeta =0$
      1. tutto uguale, ma BF e AF ora sono praticamente separate da un unico punto, in cui il modulo va all’infinito e la fase è “indeterminata” perchè compie un salto.

Considerando che moltiplicando due funzioni complesse espresse in modulo (in decibel) e fase si ottiene una funzione che ha per fase la somma delle fasi e come modulo la somma dei moduli (in decibel), si ha che se uno di questi fattori si presenta elevato a potenza $i$-esima nella funzione di trasferimento, semplicemente il suo contributo ha, nel modulo, pendenza moltiplicata per $i$, e nella fase ha pendenze e valori moltiplicati per $i$. Questo perchè è come se sommassi ogni contributo tramite un principio di sovrapposizione. In effetti, per disegnare i grafici di Bode asintotici a mano conviene proprio disegnare tutti i vari contributi indipendentemente e successivamente “sommarli graficamente”.

Invece, se il fattore si trova al numeratore della funzione di trasferimento e non al denominatore, sia i contributi dei moduli che quelli delle fasi si ribaltano (sono da moltiplicare per $-1$). In tal caso, dove prima si parlava di poli, ora si parlerà di zeri, ma il resto della trattazione resta identico.

Diagramma polare

I diagrammi polari di funzioni complesse sono praticamente rappresentazioni grafiche sul piano di Gauss (parte reale sulle ascisse, parte immaginaria sulle ordinate). Le quantità a modulo costante si trovano sulla stessa circonferenza, quelle alla stessa fase (arctan…), sulla stessa semiretta.

I diagrammi polari li facciamo guardando quelli di Bode.
Fondamentalmente, tu del diagramma polare determini “manualmente” soltanto il comportamento iniziale e finale quindi per $\omega \to 0^{+}$ e per $\omega \to +\infty$ (e anche questo, guardando Bode) e poi raccordi, sempre guardando Bode.
In particolare:

• comportamento iniziale:
  • se il sistema non ha poli nell’origine allora il diagramma polare parte da un punto sull’asse reale, avente quindi fase nulla mi pare di poter dire, e modulo iniziale che posso vedere da Bode.
  • se il sistema ha $n$ poli nell’origine (cioè presenta termini del tipo $K/s^n$) allora il diagramma polare parte da un punto infinitamente lontano dall’origine, con fase iniziale ${\phi }_{\text{in}}=-\frac{\pi }{2}\cdot n+\angle K$ dove $\angle K$ è $0$ se $K>0$ oppure $\pm \pi$ se $K<0$controllare
    • $K$ si determina facendo $K={\lim }_{s\to 0}{s}^{n}F(s)$
    • per determinare il quadrante da cui iniziare a tracciare il diagramma dopo aver calcolato la fase iniziale devi vedere dal diagramma di Bode della fase se essa diminuisce o aumenta andando dal valore iniziale al valore finale e tracciare di conseguenza.
• comportamento finale:
  • per noi, i sistemi saranno sempre strettamente propri. In questo caso, il diagramma termina sempre nell’origine.
  • la fase finale è la fase con cui arriva nell’origine ed è multipla di 90 gradi secondo ${\phi }_{\text{fin}}={\phi }_{\text{in}}-90(n_{\text{np}}+m_{\text{p}})+90(n_{\text{p}}+m_{\text{np}})$ dove $n_{\text{np}}$ è il numero di poli a parte reale non positiva (esclusi quelli nell’origine), $m_{\text{p}}$ è il numero di zeri a parte reale positiva, ecc.

Diagramma di Nyquist

Il diagramma di Nyquist alla fine è un diagramma polare, o meglio una loro estensione, infatti la pulsazione non è più solo positiva qui ma è $\in [-\infty ,+\infty ]$. Quindi che succede?

• Devi disegnare due volte il diagramma polare, quando finisci di disegnarlo devi disegnarlo ribaltato rispetto all’asse reale sullo stesso grafico e unire i valori che vanno all’infinito con semi-circonferenze che vanno in senso orario, di raggio infinito.
  • Se non hai poli nell’origine, ottieni subito un percorso chiuso.
  • Se hai $n$ poli nell’origine, devi fare $n$ semi-circonferenze.

MATLAB

Su MATLAB i diagrammi polari non ci stanno, ci sta solo il comando nyquist(F) e tra l’altro viene anche visualizzato con una brutta scala: meglio se zoommi sempre intorno all’origine per capire come stanno le cose. Inoltre, non ci saranno mai le circonferenze a raggio infinito.
Potrebbe esserti utile (ma anche no) usare axis equal dopo.

Info

Perchè va fatto così? (Lo capisce solo Gabriele sto pezzo)
Il fatto che ci sia una simmetria per cui il diagramma va disegnato ribaltato deriva dal fatto che $\omega <0$ è come dire che stiamo graficando sia $G(j\omega )$ che $G(-j\omega )$.
Il grafico di Nyquist è una “catena chiusa” perchè in teoria sta graficando la funzione $G(s)$ da $0^{+}$ a $+\infty$ e da $-\infty$ a $0^{-}$, e i punti di $0^{-}$ e $0^{+}$ sono coincidenti, così come i punti di $+\infty$ e $-\infty$.

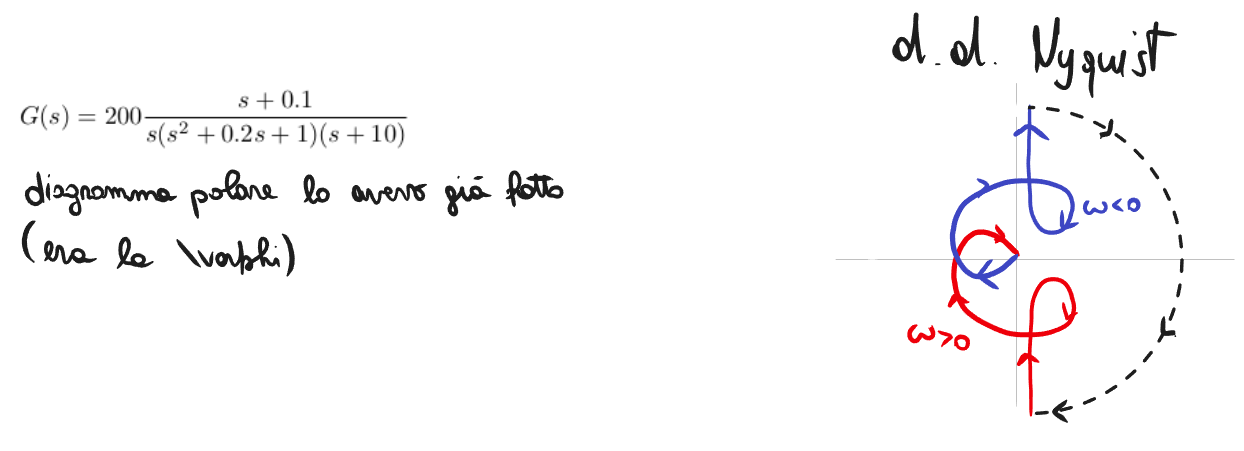
Diagramma di Nichols

È un diagramma che fondamentalmente sintetizza i diagrammi di Bode in uno solo: infatti il piano di Nichols è “fase in gradi” $\times$ “modulo in dB”.
Il suo utilizzo è meglio vederlo in IND02b.Uso dei diagrammi e margini di stabilità.