TAR14.Stabilità interna

Stabilità di un movimento

Dati:

• un movimento nominale del sistema $\tilde{x}(t)$ ottenuto applicando un ingresso nominale $\tilde{u}(t)$ posto in uno stato iniziale nominale ${\tilde{x}}_0$
• un movimento perturbato del sistema $x(t)$ ottenuto applicando lo stesso ingresso nominale $\tilde{u}(t)$, ma con la differenza che il sistema è si sarà mosso da uno stato iniziale diverso, perturbato, $x_0$
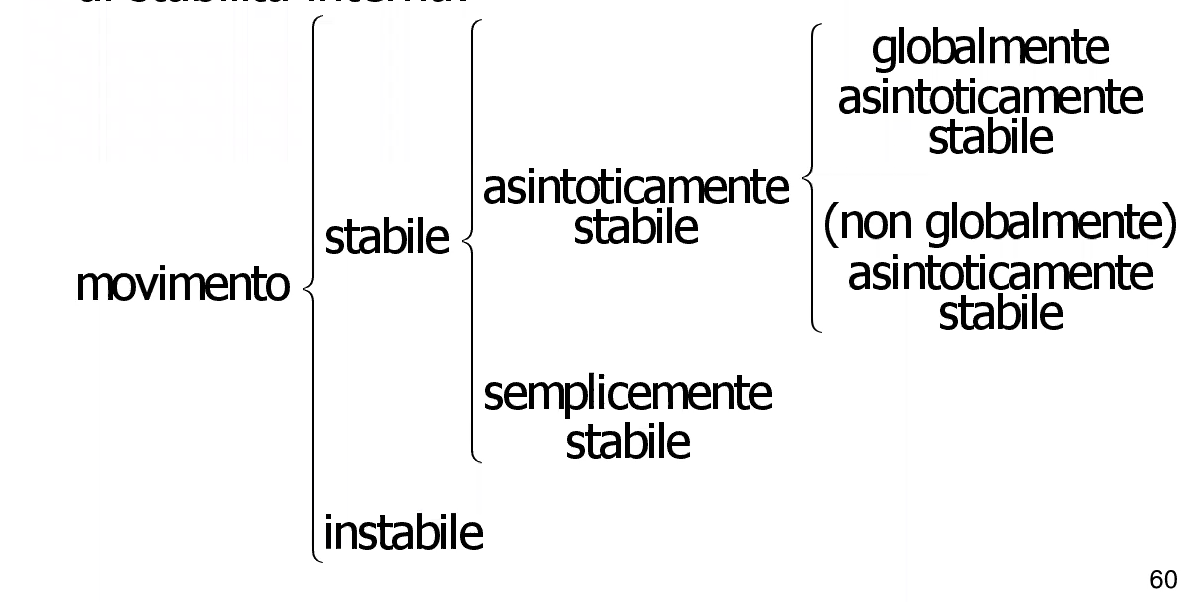
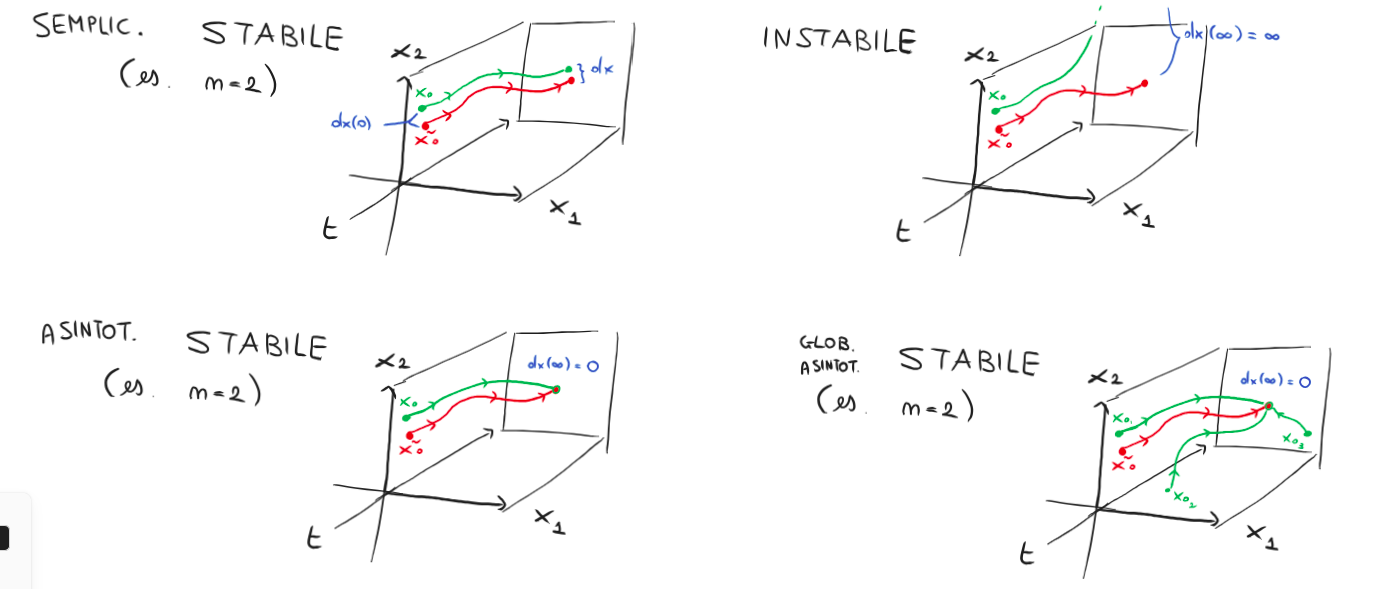
  si valuta lo scarto $x(t)-\tilde{x}(t)=\delta x(t)$ (in particolare la sua norma euclidea o infinito):
• se rimane sempre limitato nel tempo, il movimento $\tilde{x}(t)$ è detto stabile, ma mai dire stabile e basta per caratterizzare un movimento
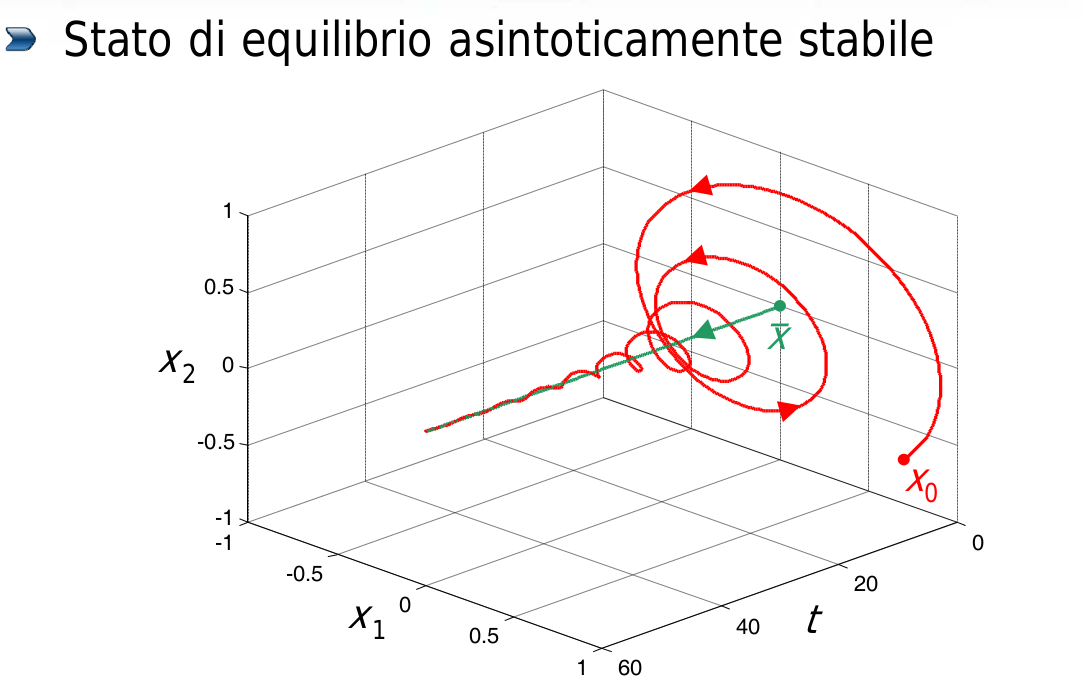
  • se la perturbazione, oltre a restare sempre limitata nel tempo, tende anche ad annullarsi spontaneamente (es. oscillazioni di un pendolo), il movimento è detto asintoticamente stabile
    • se la perturbazione tende a zero qualunque sia la perturbazione iniziale (cioè praticamente da dove parto parto, se non cambiano ingressi e parametri, finisco sempre nello stesso punto finale), il movimento è detto globalmente asintoticamente stabile
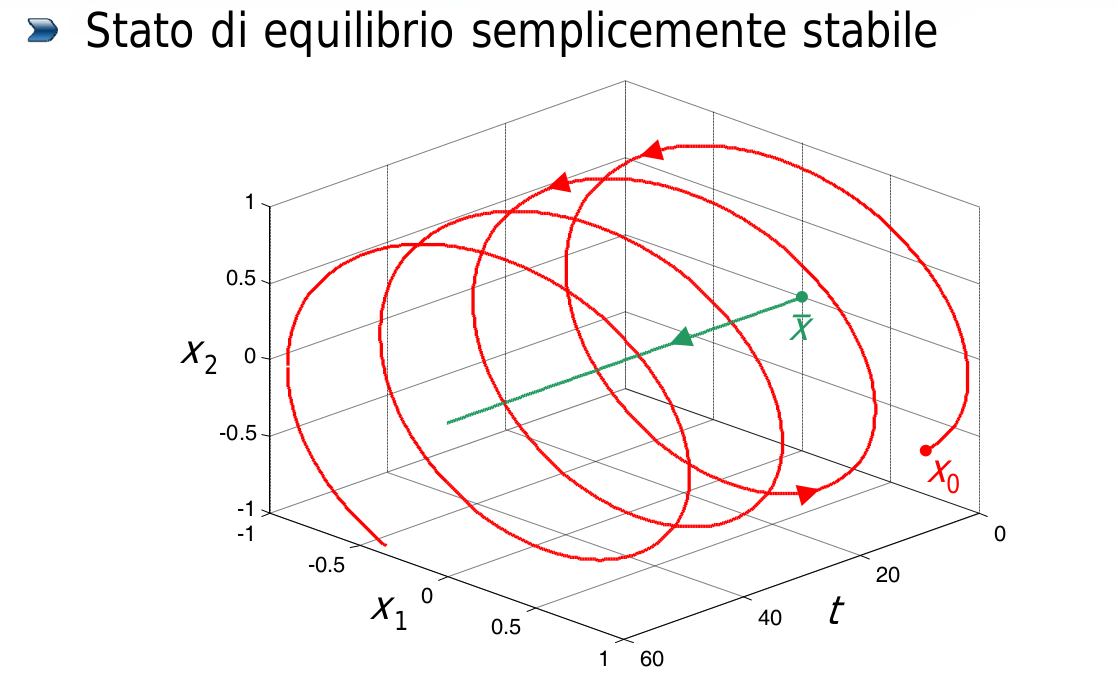
  • se la perturbazione resta sempre limitata nel tempo ma non tende ad annullarsi spontaneamente (es. oscillazioni di un pendolo senza attriti), il movimento è detto semplicemente stabile
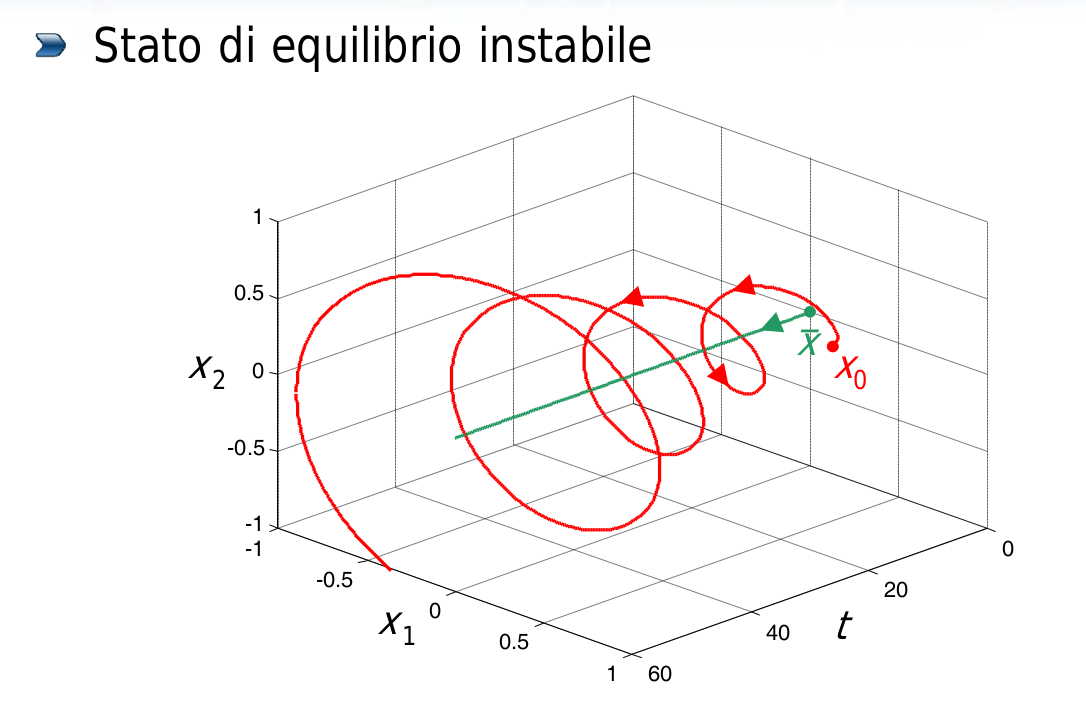
• se non rimane sempre limitato nel tempo (anzi, se diverge all’infinito), il movimento è detto instabile.

Definizione tramite limite di Lyapunov

Ricordando la definizione di continuità di una funzione (a valore reale e di variabile reale $x$) nell’intorno di un punto $x_0$: la funzione $f(x)$ è detta continua nell’intorno di $x_0$ se, per ogni $ϵ>0$, esiste un $\gamma >0$ tale che:
$\forall x\in \mathbb{R}:|x-x_0|<\gamma (ϵ)⟹|f(x)-f(x_0)|\le ϵ$
ovvero vale il limite: ${\lim }_{x\to x_0}f(x)=f(x_0)$.
In modo analogo Lyapunov definì la stabilità del movimento in questo modo:
$\forall t\in [0,+\infty ):||x_0-\widetilde{x_0}||\le \gamma ⟹|x(t)-\tilde{x}(t)|\le ϵ$

Un movimento asintoticamente stabile, oltre a soddisfare questa proprietà, soddisfa anche
${\lim }_{t\to +\infty }||x(t)-\tilde{x}(t)||=0$ (cioè si muove ma alla fine converge nello stesso punto come se non ci fosse stata nessuna perturbazione)

Per un movimento globalmente asintoticamente stabile valgono le due di cui sopra, ma la seconda vale anche $\forall x_0$.

Movimenti instabili si definiscono per esclusione.

Stabilità dell’equilibrio

Si parla di stabilità dell’equilibrio nel caso in cui il movimento nominale considerato sia uno stato di equilibrio corrispondente ad un ingresso di equilibrio.
Un sistema dinamico non lineare può presentare stati di equilibrio con caratteristiche di stabilità interna differenti ⇒ si parla di studio della stabilità “locale”.

Ad ogni stato di equilibrio asintoticamente stabile è associata una regione di attrazione (o regione di asintotica stabilità), costituita da quegli stati iniziali che danno origine a movimenti perturbati convergenti asintoticamente allo stato d’equilibrio.
In corrispondenza di un dato ingresso di equilibrio, un sistema dinamico ammette al più un unico stato di equilibrio globalmente asintoticamente stabile.

Stabilità locale di sistemi non lineari dopo linearizzazione

Niente, prima lo linearizzi e poi controlli come è il linearizzato.
Per esempio. se il linearizzato attorno ad un punto di equilibrio è semplicemente stabile, dirai che il sistema non lineare in esame presenta un movimento nominale di equilibrio semplicemente stabile.

TAR16.Stabilità interna locale dell’equilibrio di sistemi dinamici non lineari per linearizzazione

Sistemi LTI e stabilità interna del sistema

Nel caso di sistemi LTI possiamo fare lo stesso ragionamento di prima:

• prendiamo un movimento nominale $\tilde{x}$, ottenuto applicando un ingresso nominale $\tilde{u}$ al sistema, che si trovava in uno stato iniziale nominale ${\tilde{x}}_0$
• applicando lo stesso ingresso nominale $\tilde{u}$ al sistema che però si trovava in uno stato iniziale perturbato $x_0={\tilde{x}}_0+{\delta x}_0$ otterremo un movimento perturbato $x$
• possiamo valutare lo scarto tra i due movimenti: $\delta x(t)=x(t)-\tilde{x}(t)$, tuttavia qui abbiamo anche un altro modo per scriverla:
  • essendo in un sistema LTI, $\dot{\tilde{x}}=A\tilde{x}+B\tilde{u}$ e $\dot{x}=Ax+B\tilde{u}$
  • $\delta x(t)$ è soluzione dell’equazione differenziale $\dot{\delta x}=\dot{x}-\dot{\tilde{x}}$ con condizione iniziale $\delta x(0)=\delta x_0=x_0-{\tilde{x}}_0$
  • $x-\tilde{x}=Ax-A\tilde{x}=A\delta x$
  • quindi il problema di Cauchy è:
    • $\{\begin{array}{l}\dot{\delta x}(t)=A\delta x\\ \delta x(t_0=0)=x_0-{\tilde{x}}_0\end{array}$
    • e questo si risolve in $\delta x(t)=e^{At}\delta x_0$
• dato che lo scarto $\delta x$ è ciò che dobbiamo analizzare per dire se $\tilde{x}(t)$ è un movimento stabile, ma qui ci ritroviamo che $\delta x(t)=e^{At}\delta x_0$ non dipende in nessun modo da $\tilde{x}$, vuol dire che per un sistema LTI tutti i movimenti si comporteranno allo stesso modo, quindi si può dire che il sistema è stabile o meno, sottointendendo che da qualunque stato iniziale si parta, il movimento del sistema avrà sempre lo stesso comportamento in base al sistema stesso.

Dato che in $\delta x(t)=e^{At}\delta x_0$ compare la matrice esponenziale, e abbiamo già analizzato nell’analisi modale che questa espressione sarà combinazione lineare dei modi propri del sistema, possiamo concludere dicendo che per analizzare la stabilità interna di un sistema LTI è necessario analizzarne gli autovalori della matrice $A$, in modi che poi vedremo.

Tutto sto discorso, ovviamente, vale anche a tempo discreto, con le dovute modifiche alle equazioni dinamiche.