TAR15.Stabilità interna per sistemi dinamici LTI

Se hai gli autovalori

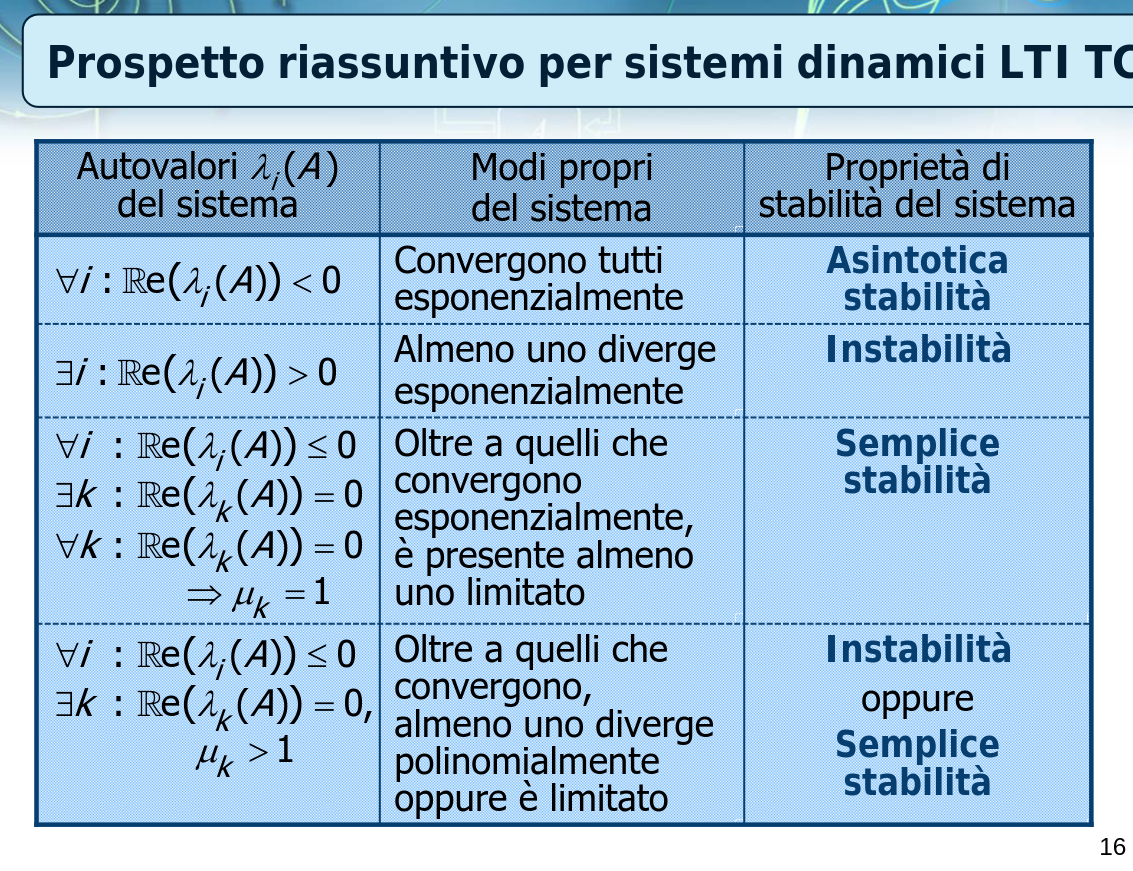
La discussione della stabilità interna di un sistema dinamico LTI si basa sugli autovalori della matrice $A$:

• caso TC
  • 
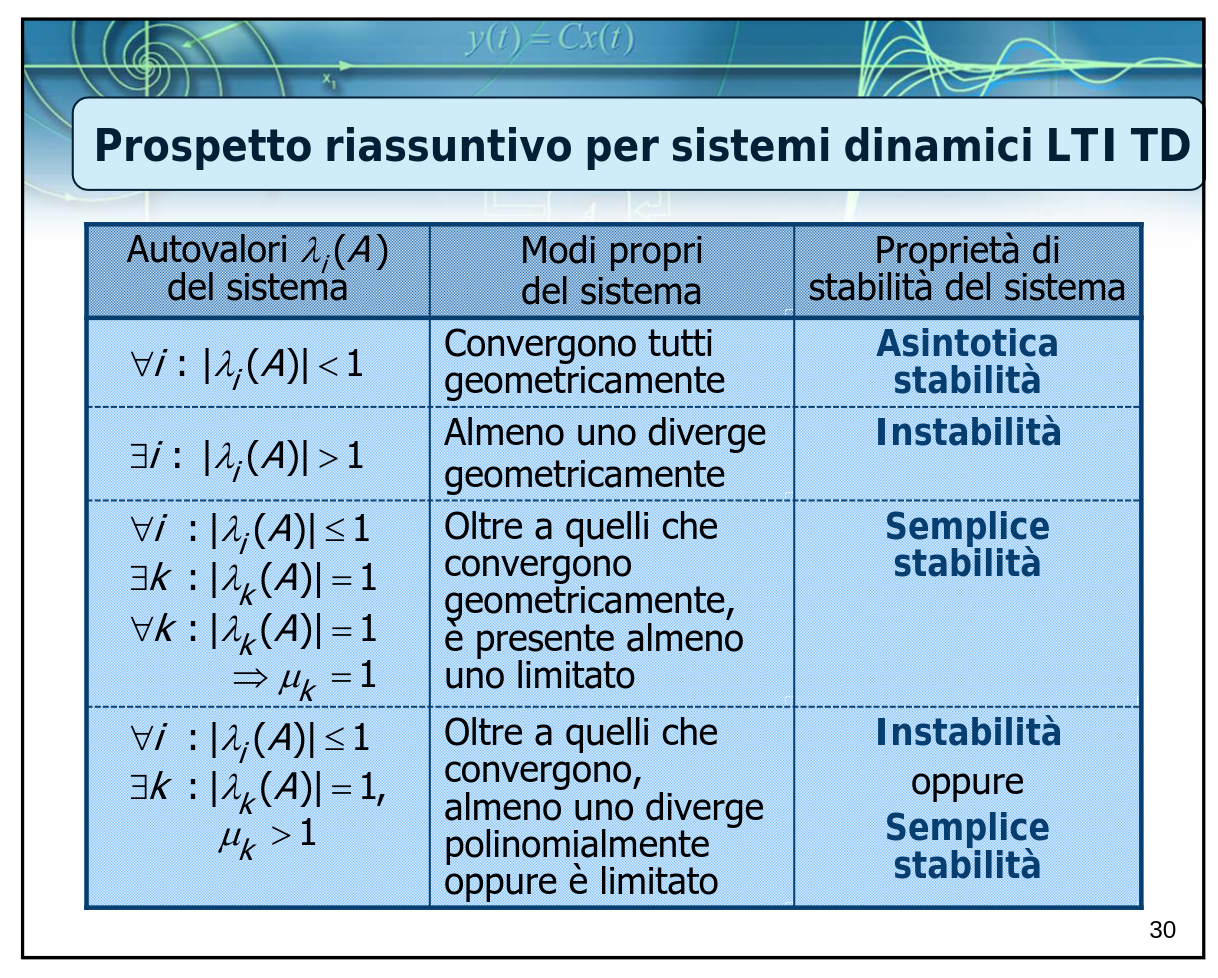
• caso TD
  • 
    Questo però vuol dire che devi fare lo sforzo di scrivere il polinomio caratteristico e anche di trovarne le radici; non è banale, infatti il polinomio caratteristico è dato da
    $p(\lambda )=\det (A-\lambda I_n)$
    e in generale può avere un grado alto.
    Questo polinomio quindi è magari facile scomporlo quando è un cubo di binomio, quando è un quadrato di binomio, quando è di secondo grado e quindi puoi usare la formula $x_{1,2}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$… ma in generale può essere una chiavica scomporlo.
    Non arriverai mai agli autovalori, sebbene hai in mano il polinomio caratteristico.

Se hai il polinomio caratteristico ma non si scompone facilmente (criteri)

Warning

Potresti pensare “vabbè, ma le radici me le faccio calcolare dalla calcolatrice”.
Ci sono due problemi:

1. La calcolatrice che abbiamo noi arriva al massimo a calcolare radici di polinomi di quarto grado.
2. Basta che in un esercizio compaia un parametro variabile al posto di uno dei coefficienti o all’interno di essi, e ti fotte, perchè servirebbe un calcolatore con calcolo simbolico.

Allora puoi usare dei criteri particolari che analizzando solo i coefficienti di un certo polinomio ti danno informazioni parziali sulle radci dello stesso. Questi criteri sono:

• criterio di Routh: la prima colonna della tabella di Routh ti da informazioni sulla presenza di radici a parte reale strettamente maggiore di $0$ - nel nostro contesto, $\Re \lambda >0⟹$ il sistema è internamente instabile. Il criterio quindi è una condizione necessaria e sufficiente affinchè il sistema a tempo continuo sia internamente asintoticamente stabile.
  • se il grado del polinomio in esame è $2$, il criterio di Routh “degenera” nella regola dei segni di Cartesio, semplicissima.
    • Nel caso di un polinomio di grado $2$, la regola dei segni di Cartesio è perfino più conveniente che usare $x_{1,2}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$; a questo punto, l’unico caso in cui ti conviene scomporre il polinomio con la calcolatrice è quando il polinomio è di grado $3$ o $4$ e non ci sono parametri variabili, ovvero nei casi in cui Cartesio non basta e dovresti fare Routh, ma la calcolatrice può ancora scomporti il polinomio caratteristico, salvandoti il culo.
  • dato che la regola dei segni di Cartesio in pratica deriva dalle prime due righe di Routh, puoi sempre controllare Cartesio prima di iniziare a costruire la tabella, in modo da non costruirla proprio se non funziona.
  • in generale, in questi criteri, ti puoi arrestare nella costruzione della tabella di Jury appena vedi che una condizione del criterio si è rotta.
• criterio di Jury: confrontare il modulo di primo e ultimo elemento della prima delle righe di ogni coppia della tabella di Jury ti dice se tutte le radici $\lambda$ del polinomio qualsiasi $p(\lambda )$ abbiano $|\lambda |<1$, che per noi vuol dire che il sistema a tempo discreto è internamente asintoticamente stabile. Prima di costruire la tabella di Jury, devi sempre verificare che le disequazioni $p(1)>0$ e $(-1{)}^{n}p(-1)>0$ siano vere (per qualche motivo).
  • se il grado del polinomio in esame è $2$, il criterio di Jury degenera ad una sola disequazione che puoi fare anche guardando soltanto il polinomio $p(\lambda )$ e senza bisogno di costruire null’altro: $|a_n|>|a_0|$
    • anche in questo caso, è più semplice nel caso di polinomio di grado $2$ fare questa cosa piuttosto che scomporre il polinomio caratteristico. Usa la calcolatrice comunque se il grade è $3$ o $4$ e non ci sono parametri variabili nei coefficienti.
  • le tre condizioni $p(1)=0$, $(-1{)}^{n}p(-1)=0$, $|a_n|>|a_0|$ bastano da sole per concludere sul polinomio di grado $2$ e per gradi superiori comunque sono la prima cosa che va fatta. Se si spacca già una di queste condizioni, non serve costruire nessuna tabella.

Regola dei segni di Cartesio (per tempo continuo)

Criterio di Routh (per tempo continuo)

• se si rompe Cartesio, è già non asintoticamente stabile (cioè se ha poli a parte reale positiva), però se non si rompe, devi controllare con il criterio di Routh.
  • dipende dalla prima colonna della tabella di Routh
  • praticamente è una tabella di cui mi interessa solo la prima colonna
    • questa è fatta da $n+1$ righe con $n$ il grado del polinomio che prendo in considerazione
    • le prime due righe si fanno semplicemente guardando il polinomio
    • per la altre righe devi seguire sto schema:
      • 
      • ogni coefficiente con pedice negativo è $0$ e tutti i coefficienti che si trovano a destra di uno $0$ sono anch’essi $0$
    • se la prima colonna della tabella di Routh ha elementi concordi allora tutte le radici del polinomio $p(\lambda )$ hanno parte reale strettamente negativa, quindi il sistema è asintoticamente stabile internamente.
      • Se la prima colonna non ha elementi nulli, tra l’altro, allora il numero di radici a parte reale positiva è uguale al numero di variazioni di segno nella tabella (come Cartesio).

Criterio di Jury (per tempo discreto)

Devi sempre usare il criterio di Jury ma assieme ad altre tre disuguaglianze, la cui ultima è semplicemente quella della prima riga di Jury.

• Per il caso $n=2$ in realtà bastano le tre disuguaglianze
  • 
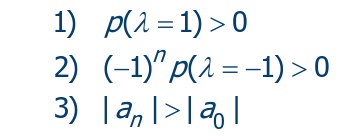
  • il criterio di Jury si basa sulla tabella di Jury che è costituita da $n-1$ coppie di righe
    • 
    • ogni coefficiente con pedice negativo è $0$ e tutti i coefficienti che si trovano a destra di uno $0$ sono anch’essi $0$
    • 
    • 
    • 
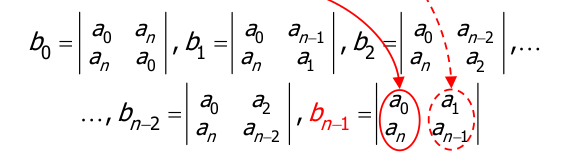
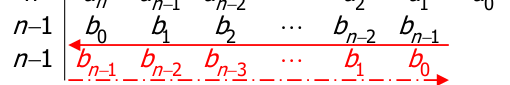
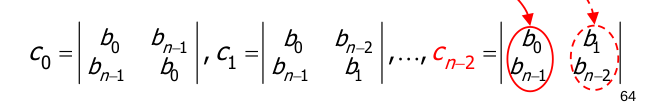
  • Il criterio dice che il polinomio $p(\lambda )$ ha tutte radici a modulo strettamente minore di $1$ se per ogni coppia di righe, guardando la prima delle due, la disequazione $|{\text{lettera riga}}_n|>|{\text{lettera riga}}_0|$ è vera.
    • $|a_n|>|a_0|$
    • $|b_n|>|b_0|$
    • $|c_n|>|c_0|$
    • $⋮$
    • $|z_n|>|z_0|$