TAR17.Raggiungibilità e controllabilità

Proprietà strutturali

Stabilità, raggiungibilità e controllabilità sono proprietà strutturali, il che significa che un sistema simile ad un sistema in esame avente una di queste proprietà la ha anch’esso.

Dire che due sistemi sono simili vuol dire che posso trasformare la matrice di stato $A$ del primo sistema in quella del secondo una trasformazione di similarità (un cambio di base).

In pratica, questo significa che le proprietà strutturali sono proprietà del sistema che dipendono unicamente dagli autovalori della matrice $A$.

Raggiungibilità

Uno stato $x^{\star }$ è detto raggiungibile dallo stato $x_0$ al tempo $t^{\star }$ se con un particolare ingresso $u^{\star }(t)$ riesco ad ottenere $x(t^{\star })=x^{\star }(t)$.

Riassunto

Se un sistema è completamente raggiungibile, è sempre possibile prevedere in quale stato il sistema si sposterà in seguito all’applicazione di un particolare ingresso. Da qui, per qualche motivo (probabilmente tramite la formula di Lagrange o roba simile), ci si sposta a dire che è possibile prevedere quale input dare al sistema perchè il suo output, quindi la risposta più che lo stato, insegua un segnale desiderato). From future: questo ci è utile per computare a priori degli ingressi da dare in pasto al sistema sapendo cosa vogliamo che lo stesso sistema dia in output.

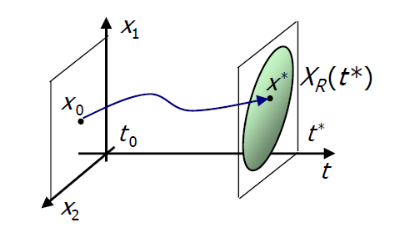
Esiste quindi un insieme di raggiungibilità $X_R(t^{\star })$ che mi racchiude tutti gli stati raggiungibili partendo dallo stato $x_0$ in un tempo finito (in particolare, $t^{\star }$).
Il sottospazio di raggiungibilità in particolare è l’insieme di raggiungibilità di cardinalità più grande (quindi c’è un tempo particolare al quale si manifesta l’insieme di dimensione massima).
Se il sottospazio di raggiungibilità è diverso dall’intero spazio dello stato (l’insieme dei possibili valori di $x$) ci sarà anche un insieme di non raggiungibilità: tali stati non sono raggiungibili in tempo finito dal sistema, per nessun ingresso.

Controllabilità

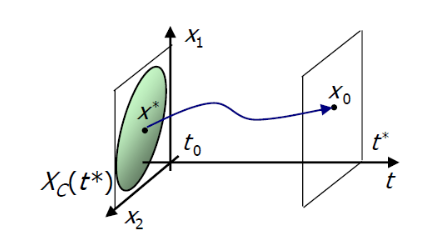
Uno stato $x^{\star }$ si dice controllabile allo stato $x_0$ al tempo $t^{\star }$ se con un particolare ingresso $u^{\star }(t)$ riesco ad ottenere $x(t^{\star })=x_0$.

Sistemi LTI

Per sistemi LTI, $X_R=X_C$, perlomeno a tempo continuo.
In sistemi a tempo discreto $X_R$ potrebbe essere un po’ più piccolo: se $A$ non è singolare, però, si ricade nel caso precedente.

Un sistema LTI completamente raggiungibile allora è anche completamente controllabile. Noi faremo riferimento alle proprietà di raggiungibilità.

Gli autovalori della matrice di stato $A$ determinano completamente l’andamento della risposta (libera) del sistema. È per questo che facciamo l’analisi modale: già analizzando gli autovalori di $A$ si possono ottenere tante informazioni sul sistema, in particolare, informazioni sulla sua stabilità.

Gli autovalori di $A$ sono da classificarsi in base alla raggiungibilità del sistema.
In un sistema LTI non completamente raggiungibile succede che alcuni autovalori della matrice $A$ sono “da associare” al sottospazio di raggiungibilità e alcuni al sottospazio di non raggiungibilità.

Sistemi LTI SISO - analisi della raggiungibilità

L’analisi sulla raggiungibilità di un sistema a singolo ingresso può essere fatta a partire dalle matrici di stato e degli ingressi. A partire da queste, si può costruire la matrice di raggiungibilità del sistema e fare un test su questa per determinare se il sistema sia completamente raggiungibile o meno.

Nel caso di un sistema con un singolo ingresso, la matrice di raggiungibilità ha la forma:
$M_R=[BAB\dots A^{n-1}B]$
dove $n$ è la $n$ della $R^{n,n}$ a cui appartiene $A$, ovver la dimensione del sistema, cioè il numero di equazioni di stato / variabili di stato.
Quando questa matrice ha rango pari ad $n$, il sistema è completamente raggiungibile.

Info

Rango e come non calcolarlo
Il rango di una matrice è il numero di righe (o colonne) linearmente indipendenti.

In pratica, significa che prendendo le righe (colonne) della matrice e trattandole come vettori separati, usandoli come una base, si può creare uno spazio vettoriale (combinando linearmente questi vettori) di dimensione pari al rango.
Rimuovendo dalla base un vettore non linearmente indipendente (quindi che si può creare come combinazione lineare degli altri), lo spazio vettoriale generato non cambia, in quanto quel vettore che ora è stato rimosse non è mai davvero stato necessario alla generazione.

Il rango di una matrice si può vedere “ad occhio” nel momento in cui è palese il rapporto che esiste tra le righe. Per esempio, in

$\left(\begin{array}{ccc}1& 2& 7\\ 2& 4& 9\\ 3& 6& 19\end{array}\right)$

Il rango è $2$, in quanto la prima e la terza colonna sono evidentemente linearmente indipendenti, mentre la colonna centrale è ricavabile moltiplicando la prima per $2$.
A volte però non è ben visibile questo rapporto, per cui il metodo più comune per il calcolo del rango prevede la riduzione della matrice (mediante mosse di Gauss).

Nel nostro caso, non è nemmeno necessario calcolare esplicitamente il rango.
L’unica informazione di cui abbiamo bisogno è sapere se questa matrice $M_R$ abbia rango $n$ oppure no.
Dato che la matrice $M_R$ ha di per sè $n$ righe, perchè si abbia rango $=n$ è necessario che si abbia rango massimo (che quindi tutte le sue righe / colonne siano linearmente indipendenti).
Una conseguenza della presenza di righe o colonne non linearmente indipendenti è che il determinante della matrice va a $0$. Quindi a noi basterà semplicemente verificare che la matrice non sia singolare.

Nel caso invece di un sistema con più di un ingresso, la matrice di raggiungibilità si costruisce come
$M_R=[BAB\dots A^{n-b}B]$
dove $b$ è il rango di $B$ (che generalmente è più semplice calcolare, ma non si sa mai davvero). In effetti, il caso con un solo ingresso ha $b=1$.

Info

La dimostrazione del perchè funziona questa cosa l’abbiamo fatta solo a TD, perchè era più facile. Comunque non l’ho scritta, non la ricordo, non penso la scriverò mai. Il senso della dimostrazione è che la matrice di raggiungibilità deve essere formata da colonne (o righe?) che formino una base ortogonale per lo spazio degli stati $x$, quindi la matrice deve essere formata da colonne (o righe?) linearmente indipendenti tra loro.

• Per generare uno spazio vettoriale come quello di $x$ che sono vettori in $n$ dimensioni, serve una base formata da $n$ vettori, quindi la matrice deve avere almeno $n$ colonne / righe.
• Se una matrice non ha rango massimo, la matrice non ha tutte le colonne (o righe?) linearmente indipendenti tra loro.
• Basi non ortogonali (almeno credo) sono composte da vettori non tutti linearmente indipendenti tra loro. Comunque usare una base del genere per generare uno spazio funziona; solo che alcuni dei vettori di questa base verranno generati a loro volta come combinazioni degli altri, quindi rimuoverli completamente dalla base non cambierebbe nulla.
  Unendo queste tre cose, si ha che una matrice di raggiungibilità, che normalmente sarebbe dipendente dal tempo, determinata ad un tempo specifico che le faccia avere $n$ colonne (a TD è facile fare questa cosa perchè si conta a passi, ma comunque andiamo avanti), e avente rango massimo ovvero determinante diverso da $0$, è una specifica sufficiente per dire che il sistema è completamente raggiungibile.

MATLAB

La matrice di raggiungibilità si può calcolare direttamente con il comando ctrb(A, B).

Realizzazione di una funzione di trasferimento secondo la forma canonica di raggiungibilità

Sostanzialmente la domanda è:

• se ho una funzione di trasferimento $H(s)$ o $H(z)$, posso costruire un sistema che la implementa?
  Sì, lo puoi fare ma ne esistono infiniti. Noi facciamo che scriverne uno solo, quello in forma canonica di raggiungibilità, che tra l’altro sarà per definizione completamente raggiungibile.
  Praticamente si costruisce “per ispezione” nel senso che guardi la funzione di trasferimento e scrivi.

Il procedimento è questo - abbastanza stupido: