TAR21.Stabilità esterna e risposta a regime

Un sistema dinamico LTI inizialmente a riposo harisposta libera nulla, quindi la sua risposta complessiva è data dalla sola risposta forzata. Si può quindi scrivere
$Y(s)=H(s)U(s)$
Partendo da questa si può dire che il sistema è detto BIBO-stabile (bounded input - bounded output) o esternamente stabile se la sua risposta forzata a ingressi limitati è sempre limitata.

Info

Forma minima
Un sistema può essere rappresentato in mille modi, ma quando un sistema è rappresentato in una forma tale che sia completamente raggiungibile e completamente osservabile è detto in forma minima. Un sistema in forma minima contiene il numero minimo di variabili di stato per descriversi.

In generale, scrivendo la funzione di trasferimento del sistema nella forma $H(s)=\frac{N(s)}{D(s)}$ tramite $H(s)=C(sI-A{)}^{-1}B+D$ avrai che le radici del denominatore, dette poli del sistema, sono in generale un sottoinsieme degli autovalori di $A$. Questo perchè potrebbero avvenire delle cancellazioni zeri-poli e quindi arriveresti ad avere una funzione di trasferimento con un numero di poli minore del numero degli autovalori.

Se il sistema è in forma minima, però, i poli coincidono esattamente con gli autovalori. Inoltre la risposta libera di un sistema in forma minima sarà sempre nulla e il sistema sarà quindi interamente descrivibile tramite la sola funzione di trasferimento tra ingresso e uscita (non esistono parti non osservabili o non raggiungibili nel sistema).

La condizione per la stabilità esterna è praticamente la stessa della stabilità interna, ma applicata solo ai poli.
Il sistema è BIBO-stabile se tutti i poli della funzione di trasferimento hanno parte reale strettamente negativa (nel caso TC) oppure modulo strettamente minore di 1 (nel caso TD).

Ci sono quindi delle implicazioni che legano i due tipi di stabilità:

• sistema (internamente) asintoticamente stabile $⟹$ tutti i suoi poli sono nella regione di asintotica stabilità $⟹$ sistema esternamente stabile
  • sistema esternamente stabile e in forma minima $⟹$ tutti i suoi poli sono nella regione di asintotica stabilità e in più i poli coincidono precisamente con gli autovalori di $A$. Quindi, paradossalmente, puoi dire che per analizzare il sistema puoi analizzare il $D(s)$ invece che il polinomio caratteristico $p(\lambda )$ di $A$.
    
    Queste implicazioni ci semplificano di parecchio il lavoro di verifica della stabilità:
• se ci viene detto che il sistema è asintoticamente stabile, è automaticamente anche esternamente stabile
• se ci viene detto che il sistema è in forma minima e ci viene data la FdT, per verificare la stabilità interna ci basta scomporre il $D(s)$ (o se non vogliamo scomporlo, possiamo usare i criteri di Cartesio, Routh o Jury) e verificare la solita condizione: così otterremo sia l’informazione sulla stabilità interna che sulla stabilità esterna
• se ci viene detto che il sistema è in forma minima e ci vengono date le matrici, per verificare la stabilità interna possiamo calcolare la $H(s)$ e verificare la solita condizione sui poli invece che cercare di calcolare gli autovalori. Ma questo è idiota come processo perchè è molto più veloce calcolare il polinomio caratteristico e al massimo usare Routh/Jury, al posto di fare $C(sI-A{)}^{-1}B+D$ e poi rischiare di dover usare comunque Routh/Jury perchè il denominatore non si scompone facilmente o ha parametri variabili
• todo forse ci sta anche qualche semplificazione se il sistema ci viene dato in forma matriciale e canonica di raggiungibilità / controllabilità, ma non ne sono sicuro.

Risposta in regime permanente

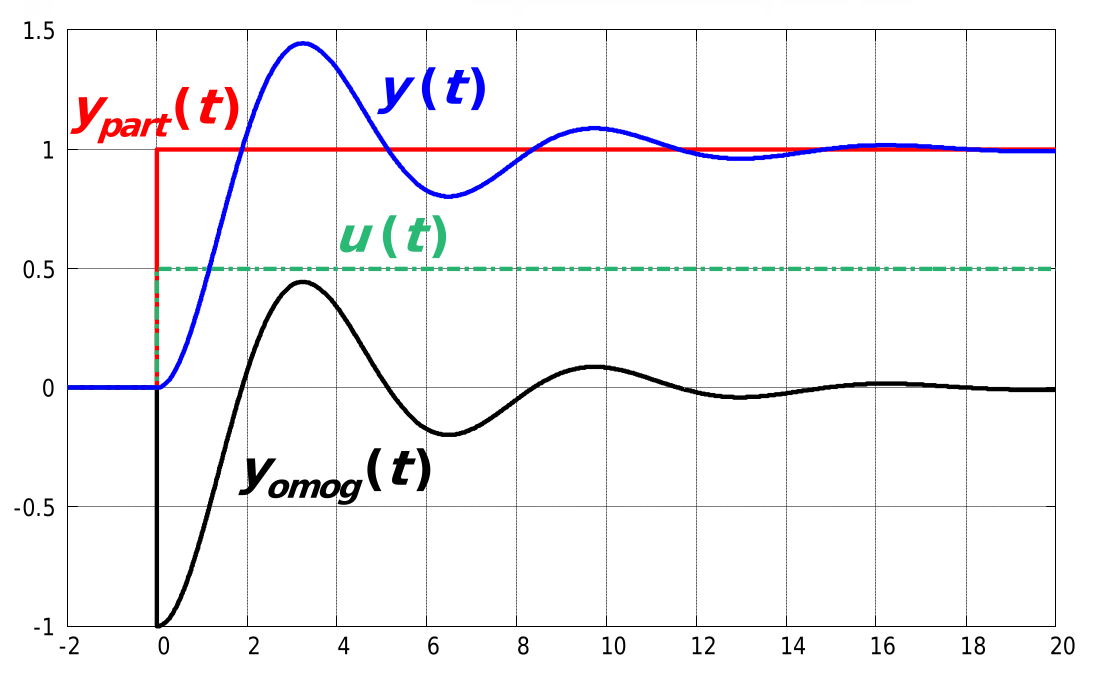
Dall’analisi modale si scopre che la $y_{\text{omogenea}}$, ovvero la risposta libera, è combinazione lineare dei modi del sistema.

Un sistema asintoticamente stabile tende, all’infinito, ad avere parti reali degli autovalori della matrice di stato nulli, e quindi una risposta libera nulla; per cui per tempi sufficientemente grandi è vero $y(t)=0+y_{\text{particolare}}(t)=y_{\text{forzata}}(t)$.
La risposta di un sistema dinamico asintoticamente stabile (o esternamente stabile e in forma minima) può allora essere divisa in un transitorio iniziale e in una risposta in regime permanente.

In pratica, il sistema non influenza la forma della risposta (le frequenze contenute nel segnale), ma le trasformazioni che applica all’ingresso sono solo in modulo (intensità del segnale) e in fase (ritardo / anticipo del segnale).

Per un ingresso di tipo gradino (quindi costante) anche la risposta in regime permanente sarà costante, al massimo scalata.

Se l’ingresso è sinusoidale, anche la risposta in regime permanente sarà sinusoidale, al massimo scalata e sfasata.